Lunar circadian rhythms
Is sleep affected by the phase of the moon? An analysis of several years of 4 Zeo users’ sleep data shows no lunar cycle.
I attempt to replicate, using public Zeo-recorded sleep datasets, a finding of a monthly circadian rhythm affecting sleep in a small sleep lab. I find only small non-statistically-significant correlations, despite being well-powered.
I happened to see some news coverage of a sleep paper entitled “Evidence that the Lunar Cycle Influences Human Sleep” ( et al 2013):
…Here we show that subjective and objective measures of sleep vary according to lunar phase and thus may reflect circalunar rhythmicity in humans. To exclude confounders such as increased light at night or the potential bias in perception regarding a lunar influence on sleep, we retrospectively analyzed sleep structure, electroencephalographic activity during non-rapid-eye-movement (NREM) sleep, and secretion of the hormones melatonin and cortisol found under stringently controlled laboratory conditions in a cross-sectional setting. At no point during and after the study were volunteers or investigators aware of the a posteriori analysis relative to lunar phase. We found that around full moon, electroencephalogram (EEG) delta activity during NREM sleep, an indicator of deep sleep, decreased by 30%, time to fall asleep increased by 5 min, and EEG-assessed total sleep duration was reduced by 20 min. These changes were associated with a decrease in subjective sleep quality and diminished endogenous melatonin levels. This is the first reliable evidence that a lunar rhythm can modulate sleep structure in humans when measured under the highly controlled conditions of a circadian laboratory study protocol without time cues…
This interested me both because of the novelty of the claim and because if lunar phase has an impact on sleep, then adding it as a covariate could increase the power of my sleep analyses by reducing error (and best of all, could be calculated for any date - without requiring data I did not collect at the time). So I looked into it further.
Background
I would summarize the key claims in et al 2013 as being (adding numbering & effect-sizes):
We found that around the full moon,
electroencephalogram (EEG) delta activity during NREM sleep, an indicator of deep sleep, decreased by 30%, [total NREM time in lunar class 1: 78.1 (2.2); class 3: 74.5 (2.5); d = 1.56]
time to fall asleep increased by 5 min [class 1: 16.3 (1.9); class 3: 12.1 (1.3); d = 2.6]
and EEG-assessed total sleep duration was reduced by 20 min. [409 (7.9); 424.8 (11); d = 1.7]
These changes were associated with a decrease in subjective sleep quality [51.2 (3.7); 56.4 (3.5); d = 1.44]
The two graphs showing patterns when plotted by lunar phase:
![“Figure 1: Time to Fall Asleep and Lunar Phase. Each data point (total of 64 nights double plotted) represents EEG-defined sleep-onset time (ie. sleep latency: time between lights off and the first EEG occurrence of stage 2 sleep in minutes). The different color-coded symbols depict the different gender and age groups: pink for young women, blue for young men, white for older women, and gray for older men. Note: a lunar-phase (pictures upper abscissa)-dependent distribution could be fitted with a sinusoid function [f = y0 + a · sin(2 · π · x⧸b + c); goodness of fit, r = 0.46]. The colored boxes delineate the moon classes 1, 2, and 3, with moon class 1 comprising nights that occurred −4 and +4 days around full moon, moon class 2 comprising nights that occurred 5 to 9 days before and after full moon, and moon class 2 comprising nights that occurred 10 to 14 days before and after full moon.”](/doc/zeo/2013-cajochen-figure1.jpg)
“Figure 1: Time to Fall Asleep and Lunar Phase. Each data point (total of 64 nights double plotted) represents EEG-defined sleep-onset time (ie. sleep latency: time between lights off and the first EEG occurrence of stage 2 sleep in minutes). The different color-coded symbols depict the different gender and age groups: pink for young women, blue for young men, white for older women, and gray for older men. Note: a lunar-phase (pictures upper abscissa)-dependent distribution could be fitted with a sinusoid function [f = y0 + a · sin(2 · π · x⧸b + c); goodness of fit, r = 0.46]. The colored boxes delineate the moon classes 1, 2, and 3, with moon class 1 comprising nights that occurred −4 and +4 days around full moon, moon class 2 comprising nights that occurred 5 to 9 days before and after full moon, and moon class 2 comprising nights that occurred 10 to 14 days before and after full moon.”
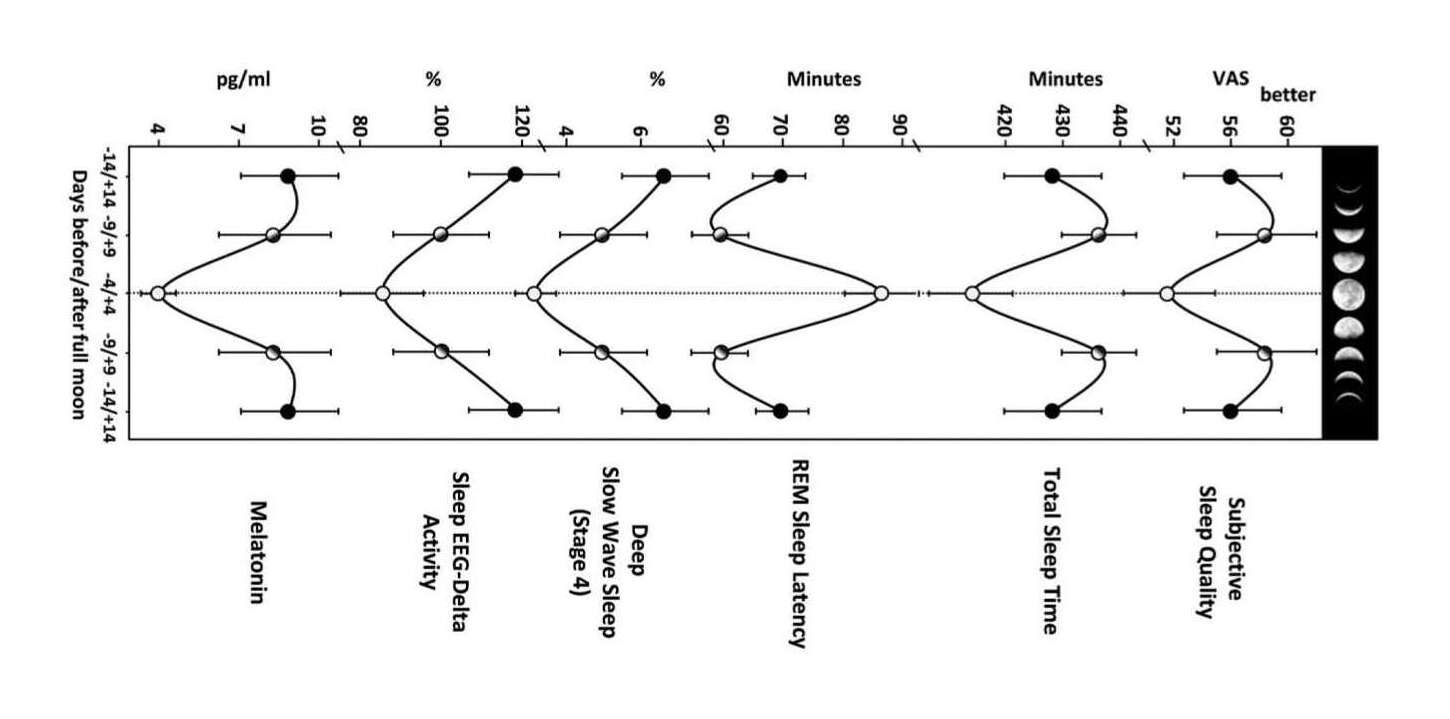
“Figure 3: The Influence of Lunar Phase on Sleep Variables and Melatonin. From top to bottom: subjective sleep quality as assessed on the Leeds Sleep Evaluation Questionnaire (LSEQ) in the morning on waking, objective total sleep time and sleep latency in minutes from PSG recordings, stage 4 sleep and occipital EEG delta activity (0.5-1.25 Hz) as a percentage of the value at 29/+9 day around full moon, and salivary melatonin levels in the evening before lights off (average of 2 hr before lights off). Mean values 6SEM (total n = 64) are shown. Data are plotted according to lunar classes: 0-4, 5-9, and 10-14 days distant from the nearest full moon phase. See also Figure S1 and Table S1.”
Reading the paper, I didn’t find it convincing. It’s a small sample size (~64 nights across 33 people), there’s a ton of measured variables they could look at for responses, some of the analysis choices are questionable (like how they binned phase of moon: why discretize it when the easy approach is to use some astronomical library to get an exact percentage visible? They never justify their “three lunar classes”), they show the scatterplot of only one of their variables which isn’t terribly impressive, there’s many possible covariates like gender & age, it’s a post-hoc analysis they admit they thought up one night (so how many other analyses did they run and not publish…?), the data is very old which makes me wonder why now & where is the rest of the data from their sleep lab, and (as they say) the priors are against there being any effect since previous research has generally failed.
As far as replications go, Eric Jain found no lunar correlation in his BodyMedia FIT data after including weather data, and et al 2014/ et al 2015 failed to replicate the result (finding no notable effects), with et al 2014 finding lunar effects but some in the opposite direction.
Fortunately, I have been using a Zeo since 201016ya, so I can attempt a replication myself. While I don’t have salivary melatonin or cortisol levels or raw EEGs, I do have all the summary metrics from my Zeo, which my latest export in January 201412ya gives me ~1050 days of data (~16x more nights, all from one subject with the reduced variability but also reduced external validity that implies). The analysis is easy enough, and I can even improve on their analysis by using a better phase variable than their arbitrary trichotomy; my life is not as well controlled as a sleep laboratory but here I have the advantage of no sleep disturbance from the laboratory or equipment an in any case, because I would be exposed to lunar cues like the full moon, we would expect the error here to be finding a relationship where there is not one due to circadian rhythms. 3 other Zeo users kindly offered me their Zeo data, giving me a total of 2431 nights of data. Hopefully with >28x more nights of data, I can find their lunar correlations - if they are real.
What would the results mean? If I found a lunar pattern, it would be consistent with their results, but on its own, it cannot prove that there is a lunar circadian pattern, since it could be due to, say, the direct effects of moonlight increasing ambient light. On the other hand, if there is no lunar pattern in the data, then that suggests that there are no lunar-related effects at all - much less a lunar circadian rhythm. (If A → C, and C, then by affirming the consequent, probabilistically A is more likely to be true; but if ~C, then ~A by modus tollens.)
Analysis
Preparation
zeo1 <- read.csv("https://gwern.net/doc/zeo/gwern-zeodata.csv"); zeo1$Subject <- 1
zeo2 <- read.csv("https://gwern.net/doc/zeo/2013-eva.csv"); zeo2$Subject <- 2
zeo3 <- read.csv("https://gwern.net/doc/zeo/2013-fred.csv"); zeo3$Subject <- 3
zeo4 <- read.csv("https://gwern.net/doc/zeo/2014-jay.csv"); zeo4$Subject <- 4
zeo5 <- read.csv("https://gwern.net/doc/zeo/2014-malcolm.csv"); zeo5$Subject <- 5
zeo <- rbind(zeo1, zeo2, zeo3, zeo4)
library(moonsun)
zeo$Julian.Date <- julian(as.Date(zeo$Sleep.Date, format="%m/%d/%Y"))
# "Percentage of bright area visible from Earth"
zeo$Phase <- sapply(zeo$Julian.Date, function(date) { moon(date)$phase })Descriptive
A high level overview is to just take the 4 key variables and plot them against fullness of moon; if there is any relationship, we should expect to see a clear trend (or at least a spike downwards at the right where 100% indicates a full or nearly full moon). Nevertheless, I, at least, see no lunar cycle in any of the graphs; plotting the raw data:
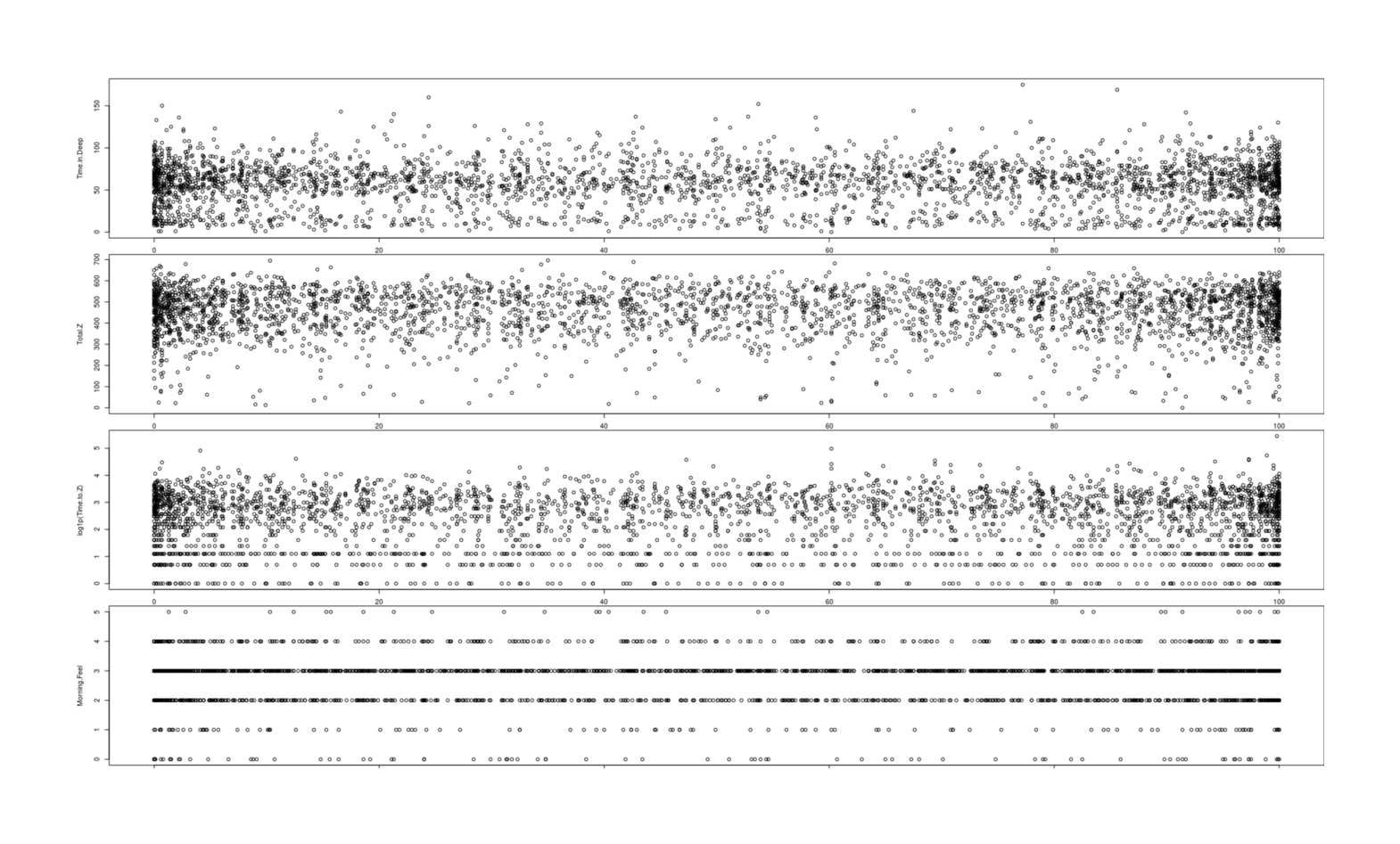
All days, by 4 sleep metrics (time in deep sleep, total sleep time, sleep latency, subjective restedness) plotted against lunar brightness
par(mfrow=c(4,1), mar=c(1,4.5,1,0))
plot(Time.in.Deep ~ Phase, data=zeo); plot(Total.Z ~ Phase, data=zeo)
plot(log1p(Time.to.Z) ~ Phase, data=zeo); plot(Morning.Feel ~ Phase, data=zeo)(There’s oversampling at 0% and 100% brightness, yes, but that merely shows the moon spends more time in being a full moon or new moon than in transitioning.)
Regressions
Walking through a bunch of statistical tests doesn’t turn up much of anything either; throwing the kitchen sink at the data, there’s a correlation of lunar brightness with total sleep time but it doesn’t reach p < 0.05.
Previously I listed the main findings for et al 2013; to map them onto the Zeo data and give them a concrete interpretation:
1 == negative correlation of
PhasewithTime.in.Deep2 == negative correlation of
PhasewithTime.to.Z3 == negative correlation of
PhasewithTotal.Z4 == negative correlation of
PhasewithMorning.Feel
Multivariate Linear Model
Pooling the 3 subjects’ data together and performing a multivariate regression with a MANOVA to correct for the correlations of the 4 response variables:
# No overall difference:
#summary(manova(cbind(Morning.Feel, Time.to.Z, Total.Z, Time.in.Deep) ~ Phase, data=zeo))
# Df Pillai approx F num Df den Df Pr(>F)
# Phase 1 0.00041310006 0.30396066 4 2942 0.87546
# Residuals 2945
## Show the specific coefficient estimates:
summary(lm(cbind(Morning.Feel, Time.to.Z, Total.Z, Time.in.Deep) ~ Phase, data=zeo))
# Response Morning.Feel :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 2.7442926613 0.0268111079 102.35656 < 2e-16
# Phase 0.0001063263 0.0004403801 0.24144 0.80923
#
# Residual standard error: 0.841041 on 2945 degrees of freedom
# (510 observations deleted due to missingness)
# Multiple R-squared: 1.979392e-05, Adjusted R-squared: -0.0003197579
# F-statistic: 0.05829426 on 1 and 2945 DF, p-value: 0.8092293
#
# Response Time.to.Z :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 16.149830041 0.426518781 37.86429 <2e-16
# Phase 0.007132688 0.007005693 1.01813 0.3087
#
# Residual standard error: 13.37952 on 2945 degrees of freedom
# (510 observations deleted due to missingness)
# Multiple R-squared: 0.0003518569, Adjusted R-squared: 1.241776e-05
# F-statistic: 1.036583 on 1 and 2945 DF, p-value: 0.3087011
#
# Response Total.Z :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 4.582213e+02 3.429405e+00 133.61542 < 2e-16
# Phase 7.715231e-03 5.632895e-02 0.13697 0.89107
#
# Residual standard error: 107.5774 on 2945 degrees of freedom
# (510 observations deleted due to missingness)
# Multiple R-squared: 6.370102e-06, Adjusted R-squared: -0.0003331863
# F-statistic: 0.01876007 on 1 and 2945 DF, p-value: 0.8910659
#
# Response Time.in.Deep :
# ...Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 55.832093248 0.843714439 66.17416 < 2e-16
# Phase 0.005127453 0.013858252 0.36999 0.71141
#
# Residual standard error: 26.46658 on 2945 degrees of freedom
# (510 observations deleted due to missingness)
# Multiple R-squared: 4.64816e-05, Adjusted R-squared: -0.0002930612
# F-statistic: 0.1368947 on 1 and 2945 DF, p-value: 0.7114145
summary(lm(cbind(Total.Z, Time.to.Z) ~ sin(2*pi*Phase), data=zeo))
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 450.142421 1.937848 232.2899 < 2e-16
# sin(2 * pi * Phase) -1.535574 2.793473 -0.5497 0.58256
#
# Residual standard error: 112.6416 on 3379 degrees of freedom
# (76 observations deleted due to missingness)
# Multiple R-squared: 8.94181e-05, Adjusted R-squared: -0.000206501
# F-statistic: 0.3021708 on 1 and 3379 DF, p-value: 0.5825611
#
# Response Time.to.Z :
# ..Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 15.5570496 0.2459476 63.25352 < 2e-16
# sin(2 * pi * Phase) -0.3217096 0.3545417 -0.90740 0.36426
#
# Residual standard error: 14.29624 on 3379 degrees of freedom
# (76 observations deleted due to missingness)
# Multiple R-squared: 0.0002436124, Adjusted R-squared: -5.226105e-05
# F-statistic: 0.8233669 on 1 and 3379 DF, p-value: 0.3642623No outcome seems associated with lunar phase, and neither sleep duration nor sleep latency have any sinusoidal relationship with lunar phase.
Multi-Level Model
This might be due to differences between subjects, so we switch to a multi-level model, treating each outcome separately. (It would be nice to do a multivariate multi-level model, but this is apparently not easy with the current state of R’s libraries.) To pick which possible MLM to use, I test with an ANOVA comparing them on the outcome variable which came closest to reaching statistical-significance, Total.Z:
library(lme4)
l1 <- lmer(Total.Z ~ Phase + (1|Subject), data=zeo)
l2 <- lmer(Total.Z ~ (Phase|Subject), data=zeo)
l3 <- lmer(Total.Z ~ (Phase+1|Subject), data=zeo)
l4 <- lmer(Total.Z ~ Phase + (Phase+1|Subject), data=zeo)
anova(l1,l2,l3,l4)
# Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
# l1 4 40886.117 40910.621 -20439.059 40878.117
# l2 5 40887.975 40918.605 -20438.988 40877.975 0.14216 1 0.70614
# l3 5 40887.975 40918.605 -20438.988 40877.975 0.00000 0 1.00000
# l4 6 40889.400 40926.156 -20438.700 40877.400 0.57515 1 0.44822
summary(l1)
# ...Random effects:
# Groups Name Variance Std.Dev.
# Subject (Intercept) 2884.257 53.70528
# Residual 10374.877 101.85714
# Number of obs: 3381, groups: Subject, 4
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 424.44039955 27.05382537 15.68874
# Phase -0.02086622 0.04969559 -0.41988
#
# Correlation of Fixed Effects:
# (Intr)
# Phase -0.091l4 comes closest, but the simplest model l1 is still the best: a fixed effect for Phase, and subject-specific intercepts. So, subject variability does not seem to be masking any lunar effect.
Power Analysis
A final consideration: was the sample size large enough to detect the correlations that et al 2013 found? For example, Total.Z seemed to come near statistical-significance, could it be that with more data, we would reach the same conclusion?
One way to approach the power analysis would be to take the data, force onto it the claimed relationship (minus 20 minutes at the full moon, and progressively less with less lunar visibility, as a linear relationship for simplicity), and see in how many replicates the multivariate linear model’s estimate for Total.Z would turn up statistically-significant with a p-value < 0.05. The power turns out to be >90%:
set.seed(1111)
library(boot)
lunar <- function(dt, indices) {
d <- dt[indices,] # allows boot to select subsample
# scale the total sleep variable by phase and the effect size from Cajochen
weight <- d$Phase / 100
d$Total.Z <- d$Total.Z - (20 * weight)
l <- summary(lm(cbind(Morning.Feel, Time.to.Z, Total.Z, Time.in.Deep) ~ Phase, data=d))
pval <- (l$"Response Total.Z")$coefficients[8]
return(pval)
}
bs <- boot(data=zeo, statistic=lunar, R=10000, parallel="multicore", ncpus=8)
# how often did the linear model produce _p_ < 0.05?
sum(bs$t < 0.05) / length(bs$t)
# [1] 0.9287At 93% power, sample size is not an issue.