Embryo editing for intelligence
Preliminary draft notes towards a cost-benefit analysis of CRISPR-based editing for complex human traits with 2015–2016 SOTAs; obsolete.
Obsolete & Abandoned
The below are rough sketches, which I do not intend to ever expand out to a complete analysis.
The initial 2016 analysis being attempted here has been obsoleted by time and later work—particularly “Heritable polygenic editing: the next frontier in genomic medicine?”, et al 2025.
Embryo Editing
One approach not discussed in Shulman & Bostrom is embryo editing, which has compelling advantages over selection:
Embryo selection must be done collectively for any meaningful gains, so one must score all viable embryos; while editing can potentially be done singly, editing only the embryo being implanted, and no more if that embryo yields a birth.
Further, a failed implantation is a disaster for embryo selection, since it means one must settle for a possibly much lower scoring embryo with little or no gain while still having paid upfront for selection; on the other hand, the edit gains will be largely uniform across all embryos and so the loss of the first embryo is unfortunate (since it means another set of edits and an implantation will be necessary) but not a major setback.
Embryo selection suffers from the curse of thin tails and being unable to start from a higher mean (except as part of a multi-generational scheme): one takes 2 steps back for every 3 steps forward, so for larger gains, one must brute-force them with a steeply escalating number of embryos.
Embryo selection is constrained by the broad-sense heritability, and the number of available embryos.
No matter how many GWASes are done on whole-genomes or fancy algorithms are applied, embryo selection will never surpass the upper bound set by a broad-sense heritability 0.8; while the effects of editing has no known upper bound either in terms of existing population variation, as there appear to be thousands of variants inclusive of all genetic changes, and evolutionarily novel changes could theoretically be made as well1 (a bacteria or a chimpanzee is, after all, not simply a small human who refuses to talk).
Editing is also largely independent of the number of embryos, since each embryo can be edited about as much as any other, and as long as one has enough embryos to expect a birth, more embryos make no difference.
Editing scales linearly and smoothly by going to the root of the problem, rather than difficulty increasing exponentially in gain - an example:
as calculated above, the et al 2013 polygenic score can yield a gain no greater than 2.58 IQ points with 1-in-10 selection, and in practice, we can hardly expect more than 0.14-0.56 IQ points in practice due to fewer than 10 embryos usually being viable etc. But with editing, we can do better: the same study reported 3 SNP hits (rs9320913, rs11584700, rs4851266) each predicting +1 month of schooling, the largest effects translating to ~0.5IQ points (the education proxy makes the exact value a little tricky but we can cross-check with other GWASes which regressed directly on fluid intelligence, like et al 2015’s whose largest hit, rs10457441, does indeed have a reported beta of -0.0324SD or -0.486) with fairly even balanced frequencies around 50% as well.2 So one can see immediately that if an embryo is sequenced & found to have the bad variant on any of those SNPs, a single edit has the same gain as the entire embryo selection process! Unlike embryo selection, there is no inherent reason an editing process must stop at one edit - and with two edits, one doesn’t even need to sequence in the first place, as the frequency means that the expected value of editing the SNP is 0.25 points and so two blind edits would have the same gain! Continuing, the gains can stack; taking the 15 top hits from et al 2015’s Supplementary Table S3, 15 edits would yield 6.35 points and yes, combined with the next 15 after that would yield ~14 points, blowing past the SNP embryo selection upper bounds. While on average any embryo would not need half of those edits, that just means that an editing procedure will go down another entry down the list and edit that instead (given a budget of 15 edits, one might wind up editing, say #30). Since the estimated effects do not decline too fast and frequencies are high, this is similar to if we skipped every other edit and so the gains are still substantial:
davies2015 <- data.frame(Beta=c(-0.0324, 0.0321, -0.0446, -0.032, 0.0329, 0.0315, 0.0312, 0.0312, -0.0311, -0.0315, -0.0314, 0.0305, 0.0309, 0.0306, 0.0305, 0.0293, -0.0292, -0.0292, -0.0292, 0.0292, -0.0292, 0.0292, -0.0291, -0.0293, -0.0293, 0.0292, -0.0296, -0.0293, -0.0291, 0.0296, -0.0313, -0.047, -0.0295, 0.0295, -0.0292, -0.028, -0.0287, -0.029, 0.0289, 0.0302, -0.0289, 0.0289, -0.0281, -0.028, 0.028, -0.028, 0.0281, -0.028, 0.0281, 0.028, 0.028, 0.028, -0.029, 0.029, 0.028, -0.0279, -0.029, 0.0279, -0.0289, -0.027, 0.0289, -0.0282, -0.0286, -0.0278, -0.0279, 0.0289, -0.0288, 0.0278, 0.0314, -0.0324, -0.0288, 0.0278, 0.0287, 0.0278, 0.0277, -0.0287, -0.0268, -0.0287, -0.0287, -0.0272, -0.0277, 0.0277, -0.0286, -0.0276, -0.0267, 0.0276, -0.0277, 0.0284, 0.0277, -0.0276, 0.0337, 0.0276, 0.0286, -0.0279, 0.0282, 0.0275, -0.0269, -0.0277), Frequency=c(0.4797, 0.5199, 0.2931, 0.4803, 0.5256, 0.4858, 0.484, 0.4858, 0.4791, 0.4802, 0.4805, 0.487, 0.528, 0.5018, 0.5196, 0.5191, 0.481, 0.481, 0.4807, 0.5191, 0.4808, 0.5221, 0.4924, 0.3898, 0.3897, 0.5196, 0.3901, 0.3897, 0.4755, 0.4861, 0.6679, 0.1534, 0.3653, 0.6351, 0.6266, 0.4772, 0.3747, 0.3714, 0.6292, 0.6885, 0.668, 0.3319, 0.3703, 0.3696, 0.6307, 0.3695, 0.6255, 0.3695, 0.3559, 0.6306, 0.6305, 0.6309, 0.316, 0.684, 0.631, 0.3692, 0.3143, 0.631, 0.316, 0.4493, 0.6856, 0.6491, 0.6681, 0.3694, 0.3686, 0.6845, 0.3155, 0.6314, 0.2421, 0.7459, 0.3142, 0.3606, 0.6859, 0.6315, 0.6305, 0.3157, 0.5364, 0.3144, 0.3141, 0.5876, 0.3686, 0.6314, 0.3227, 0.3695, 0.5359, 0.6305, 0.3728, 0.3318, 0.3551, 0.3695, 0.2244, 0.6304, 0.6856, 0.6482, 0.6304, 0.6304, 0.4498, 0.6469)) davies2015$Beta <- abs(davies2015$Beta) sum(head(davies2015$Beta,n=30))*15 # [1] 13.851 editSample <- function(editBudget) { head(Filter(function(x){rbinom(1, 1, prob=davies2015$Frequency)}, davies2015$Beta), n=editBudget) } mean(replicate(1000, sum(editSample(30) * 15))) # [1] 13.534914Editing can be done on low-frequency or rare variants, whose effects are known but will not be available in the embryos in most selection instances.
For example, George Church lists 10 rare mutations of large effect that may be worth editing into people:
To which I would add: sleep duration, quality, morningness-eveningness, and resistance to sleep deprivation ( et al 2012) are, like most traits, heritable. The extreme case is that of “short-sleepers”, the ~1% of the population who normally sleep 3-6h; they often mention a parent who was also a short-sleeper, short sleep starting in childhood, that ‘over’ sleeping is unpleasant & they do not fall asleep faster & don’t sleep excessively more on weekends (indicating they are not merely chronically sleep-deprived), and are anecdotally described as highly energetic multi-taskers, thin, with positive attitudes & high pain thresholds ( et al 2001) without any known health effects or downsides in humans4 or mice (aside from, presumably, greater caloric expenditure).
Some instances of short-sleepers are due to DEC2, with a variant found in short-sleepers vs controls (6.25h vs 8.37h, -127m) and the effect confirmed by knockout-mice ( et al 2010); another short-sleep variant was identified in a discordant twin pair with an effect of -64m ( et al 2014). DEC2/BHLHE41 SNPs are also rare (for example, 3 such SNPs have frequencies of 0.08%, 3%, & 5%). Hence, selection would be almost entirely ineffective, but editing is easy.
As far as costs and benefits go, we can observe that being able to stay awake an additional 127 minutes a day is equivalent to being able to live an additional 7 years, 191 minutes to 11 years; to negate that, any side-effect would have to be tantamount to lifelong smoking of tobacco.
The largest disadvantage of editing, and the largest advantage of embryo selection, is that selection relies on proven, well-understood known-priced PGD technology already in use for other purposes; while the former hasn’t existed and has been science fiction, not fact.
Genome Synthesis
The cost of CRISPR editing will scale roughly as the number of edits: 100 edits will cost 10x 10 edits. It may also scale superlinearly if each edit makes the next edit more difficult. This poses challenges to profitable editing since the marginal gain of each edit will keep decreasing as the SNPs with largest effect sizes are edited first - it’s hard to see how 500 or 1000 edits would be profitable. Similar to the daunting cost of iterated embryo selection, where the IES is done only once or a few times and then gametes are distributed en masse to prospective parents to amortize per-child costs to small amounts, one could imagine doing the same thing for a heavily CRISPR-edited embryo.
But at some point, doing many edits raises the question of why you are bothering with the wild type genome? Couldn’t you just create a whole human genome from scratch incorporating every possible edit? Synthesize a whole genome’s DNA and incorporate all edits one wishes; in the design phase, take the GWASes for a wide variety of traits and set each SNP, no matter how weakly estimated, to the positive direction; in copying in the data of regions with rare variants, they are probably harmful and can be erased with the modal human base-pairs at those positions, for systematic health benefits across most diseases; or to imitate iterative embryo selection, which exploits the tagging power of SNPs to pull in the beneficial rare variants, copy over the haplotypes for beneficial SNPs which might be tagging a rare variant. Between the erasing of mutation load and exploiting all common variants simultaneously, the results could be a staggering phenotype.
DNA synthesis, synthesizing a strand of DNA base-pair by base-pair, has long been done, but generally limited to a few hundred BPs, which is much less than the 23 human chromosomes’ collective ~3.3 billion BP. Past work in synthesizing genomes has included Craig Venter’s minimal bacterium in 2008 with 582,970 BP; https://www.nature.com/articles/news.2008.522 1.1 million BP in 2010 https://www.nature.com/articles/news.2010.253 483,000 BP and 531,000 BP in 2016 https://www.nature.com/articles/531557a (spending somewhere ~$40m on these projects) 272,871 in 2014 (1 yeast chromosome; 90k BP costing $50k at the time) and plans for synthesizing the whole yeast genome in 5 years https://www.nature.com/articles/nature.2014.14941 https://science.sciencemag.org/content/290/5498/1972 https://science.sciencemag.org/content/329/5987/52 https://science.sciencemag.org/content/342/6156/357 https://science.sciencemag.org/content/333/6040/348 2,750,000 BP in 2016 for E. coli https://www.nature.com/articles/nature.2016.20451 “Design, synthesis, and testing toward a 57-codon genome”, et al 2016 https://science.sciencemag.org/content/353/6301/819
https://www.quora.com/How-many-base-pairs-of-DNA-can-I-synthesize-for-1-dollar
The biggest chromosome is #1, with 8.1% of the base-pairs or 249,250,621; the smallest is #21, 1.6%, or 48,129,895. DNA synthesis prices drop each year in an exponential decline (if not remotely as fast as the DNA sequencing cost curve), and so 2016 synthesizing costs have reached <$0.3; let’s say $0.25/BP.
Chromosome |
Length in base-pairs |
Fraction |
Synthesis cost at $0.25/BP |
|---|---|---|---|
1 |
249,250,621 |
0.081 |
$62,312,655 |
2 |
243,199,373 |
0.079 |
$60,799,843 |
3 |
198,022,430 |
0.064 |
$49,505,608 |
4 |
191,154,276 |
0.062 |
$47,788,569 |
5 |
180,915,260 |
0.058 |
$45,228,815 |
6 |
171,115,067 |
0.055 |
$42,778,767 |
7 |
159,138,663 |
0.051 |
$39,784,666 |
8 |
146,364,022 |
0.047 |
$36,591,006 |
9 |
141,213,431 |
0.046 |
$35,303,358 |
10 |
135,534,747 |
0.044 |
$33,883,687 |
11 |
135,006,516 |
0.044 |
$33,751,629 |
12 |
133,851,895 |
0.043 |
$33,462,974 |
13 |
115,169,878 |
0.037 |
$28,792,470 |
14 |
107,349,540 |
0.035 |
$26,837,385 |
15 |
102,531,392 |
0.033 |
$25,632,848 |
16 |
90,354,753 |
0.029 |
$22,588,688 |
17 |
81,195,210 |
0.026 |
$20,298,802 |
18 |
78,077,248 |
0.025 |
$19,519,312 |
19 |
59,128,983 |
0.019 |
$14,782,246 |
20 |
63,025,520 |
0.020 |
$15,756,380 |
21 |
48,129,895 |
0.016 |
$12,032,474 |
22 |
51,304,566 |
0.017 |
$12,826,142 |
X |
155,270,560 |
0.050 |
$38,817,640 |
Y |
59,373,566 |
0.019 |
$14,843,392 |
total |
3,095,693,981 |
1.000 |
$773,923,495 |
So the synthesis of one genome in 2016, assuming no economies of scale or further improvement, would come in at ~$773m. This is a staggering but finite and even feasible amount: the original Human Genome Project cost ~$3b, and other large science projects like the LHC, Manhattan Project, ITER, Apollo Program, ISS, the National Children’s Study etc. have cost many times what 1 human genome would.
https://en.wikipedia.org/wiki/Genome_Project-Write https://www.nature.com/articles/nature.2016.20028 /doc/genetics/genome-synthesis/2016-boeke.pdf https://www.science.org/doi/10.1126/science.aaf6850 https://www.nytimes.com/2016/06/03/science/human-genome-project-write-synthetic-dna.html https://diyhpl.us/wiki/transcripts/2017-01-26-george-church/ https://www.wired.com/story/live-forever-synthetic-human-genome/ https://medium.proto.life/andrew-hessel-human-genome-project-write-d15580dd0885 “Is the World Ready for Synthetic People?: Stanford bioengineer Drew Endy doesn’t mind bringing dragons to life. What really scares him are humans.” https://medium.com/neodotlife/q-a-with-drew-endy-bde0950fd038 https://www.chemistryworld.com/features/step-by-step-synthesis-of-dna/3008753.article
Church is optimistic: maybe even $100k/genome by 2037 https://www.wired.co.uk/article/human-genome-synthesise-dna “Humans 2.0: these geneticists want to create an artificial genome by synthesising our DNA; Scientists intend to have fully synthesised the genome in a living cell - which would make the material functional - within ten years, at a projected cost of $1 billion” > But these are the “byproducts” of HGP-Write, in Hessel’s view: the project’s true purpose is to create the impetus for technological advances that will lead to these long-term benefits. “Since all these [synthesis] technologies are exponentially improving, we should keep pushing that improvement rather than just turning the crank blindly and expensively,” Church says. In 20 years, this could cut the cost of synthesising a human genome to $100,000, compared to the $12 billion estimated a decade ago.
The benefit of this investment would be to bypass the death by a thousand cuts of CRISPR editing and create a genome with an arbitrary number of edits on an arbitrary number of traits for the fixed upfront cost. Unlike multiple selection, one would not need to trade off multiple traits against each other (except for pleiotropy); unlike editing, one would not be limited to making only edits with a marginal expected value exceeding the cost of 1 edit. Doing individual genome syntheses will be out of the question for a long time to come, so genome synthesis is like IES in amortizing its cost over prospective parents.
The “2013 Assisted Reproductive Technology National Summary Report” says ~10% of IVF cycles use donor eggs, and a total of 67996 infants, implying >6.7k infants conceived with donor eggs, embryos, or sperm (sperm is not covered by that report) and were only half or less related to their parents. What immediate 1-year return over 6.7k infants would justify spending $773m? Considering just the low estimate of IQ at $3,270/point and no other traits, that would translate to (773m/6.7k) / 3270 = 35 IQ points or at an average IQ gain of 0.1 points, the equivalent of 350 causal edits. This is doable. If we allow amortization at a high discount rate of 5% and reuse the genome indefinitely for each year’s crop of 6.7k infants, then we need at least X IQ points where ((x*3270*6700) / log(1.05)) - 773000000 >= 0; x >= 1.73 or at ~0.1 points per edit, 18 edits. We could also synthesize only 1 chromosome and pay much less upfront (but at the cost of a lower upper bound, as GCTA heritability/length regressions and GWAS polygenic score results indicates that intelligence and many other complex traits are spread very evenly over the genome, so each chromosome will harbor variants proportional to its length).
The causal edit problem remains but at 12% causal rates, 18 causal edits can easily be made with 150 edits of SNP candidates, which is less than already available. So at first glance, whole genome synthesis can be profitable with optimization of only one trait using existing GWAS hits, and will be extremely profitable if dozens of traits are optimized and mutation load minimized.
How much profitable? …see embryo selection calculations… At 70 SDs and 12% causal, then the profit would be 70*15*3270*0.12*6700 - 773000000 = $1,987,534,000 the first year or NPV of $55,806,723,536. TODO: only half-relatedness
TODO:
model DNA synthesis cost curve; when can we expect a whole human genome to be synthesizable with a single lab’s resources, like $1m/$5m/$10m? when does synthesis begin to look better than IES?
eyeballing https://www.science.org/doi/10.1126/science.aaf6850 , 0.01/$ or 100$ in 1990, 3/$ or 0.3$ in 2015?
synthesis <- data.frame(Year=c(1990,2015), Cost=c(100, 0.33)) summary(l <- lm(log(Cost) ~ Year, data=synthesis)) prettyNum(big.mark=",", round(exp(predict(l, data.frame(Year=c(2016:2040), Cost=NA))) * 3095693981)) # 1 2 3 4 5 6 7 8 9 10 11 12 13 # "812,853,950" "646,774,781" "514,628,265" "409,481,413" "325,817,758" "259,247,936" "206,279,403" "164,133,195" "130,598,137" "103,914,832" "82,683,356" "65,789,813" "52,347,894" # 14 15 16 17 18 19 20 21 22 23 24 25 # "41,652,375" "33,142,123" "26,370,653" "20,982,703" "16,695,599" "13,284,419" "10,570,198" "8,410,536" "6,692,128" "5,324,818" "4,236,872" "3,371,211"As the cost appears to be roughly linear in chromosome length, it would be possible to scale down synthesis projects if an entire genome cannot be afforded.
For example, IQ is highly polygenic and the relevant SNPs & causal variants are spread fairly evenly over the entire genome (as indicated by the original GCTAs show SNP heritability per chromosome correlates with chromosome length, and location of GWAS hits), so one could instead synthesize a chromosome accounting for ~1% of basepairs which will carry 1% of variants at 1% of the total cost.
So if a whole genome costs $1b, there are ~10,000 variants, with an average effect of ~0.1 IQ points and a frequency of 50%, then for $10m one could create a chromosome which would improve over a wild genome’s chromosome by
10000 * 0.01 * 0.5 * 0.1 = 5points; then as resources allow and the synthesis price keeps dropping, create a second small chromosome for another 5 points, and so on with the bigger chromosomes for larger gains.
“Large-scale de novo DNA synthesis: technologies and applications”, 2014 https://arep.med.harvard.edu/pdf/Kosuri_Church_201412ya.pdf
Cost curve:
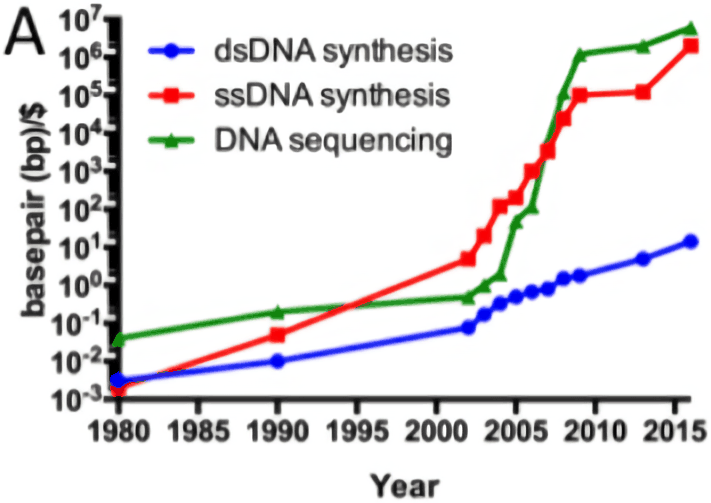
Historical cost curves of genome sequencing & synthesis, 1980–35201511ya (log scale)
“Bricks and blueprints: methods and standards for DNA assembly” http://scienseed.com/clients/tomellis/wp-content/uploads/201511ya/08/BricksReview.pdf et al 2015
‘Leproust says that won’t always be the case-not if her plans to improve the technology work out. “In a few years it won’t be $131,404.13$100,0002018 to store that data,” she says. “It will be 10 cents.”’ https://www.technologyreview.com/s/610717/this-company-can-encode-your-favorite-song-in-dnafor-100000/ April 2018
http://www.synthesis.cc/synthesis/2016/03/on_dna_and_transistors
Questions: what is the best way to do genome synthesis? Lots of possibilities:
can do one or more chromosomes at a time (which would fit in small budgets)
optimize 1 trait to maximize PGS SNP-wise (but causal tagging/LD problem…)
optimize 1 trait to maximize haplotype PGS
optimize multiple traits with genetic correlations and unit-weighted
multiple trait, utility-weighted
limited optimization:
partial factorial trial of haplotypes (eg. take the maximal utility-weighted, then flip a random half for the first genome; flip a different random half for the second genome; etc.)
this could be used for response-surface estimation: to try to estimate where additivity breaks down and genetic correlations change substantially
constrained optimization of haplotypes: maximize the utility-weight subject to a soft constraint like total phenotype increases of >2SD on average (eg. if there are 10 traits, allow +20SD of total phenotype change); or a hard constraint, like no trait past >5SD (so at least a few people to ever live could have had a similar PGS value on each trait)
because of how many real-world outcomes are log-normally distributed and the component normals have thin tails, it will be more efficient to increase 20 traits by 1SD than 1 trait by 20SD to optimize the leaky pipeline
modalization: simply take the modal human genome, implicitly reaping gains from removing much mutation load
partial optimization of a prototype genome: select some exemplar genome as a baseline, like a modal genome or very accomplished or very intelligent person, and optimize only a few SD up from that
“dose-ranging study”: multiple genomes optimized to various SDs or various hard/soft constraints, to as quickly as possible estimate the safe extreme (eg. +5 vs 10 vs 15 SD)
exotic changes: adding very rare variants like the short-sleeper or myostatin; increasing CNVs of genes differing between humans and chimpanzees; genome with all codons recorded to make viral infection impossible
CRISPR
The past 5 years have seen major breakthroughs in cheap, reliable, general-purpose genetic engineering & editing using CRISPR, since the 2012 demonstration that it could edit cells, including human ones ( et al 2013).5 Commentary in 201214ya and 201313ya regarded prospects for embryo editing as highly remote6 Even as late as July 201412ya, coverage was highly circumspect, with vague musing that “Some experiments also hint that doctors may someday be able to use it to treat genetic disorders”; successful editing of zebrafish ( et al 2013), monkey, and human embryos was already being demonstrated in the lab, and human trials would begin 2-3 years later. (Surprisingly, Shulman & Bostrom do not mention CRISPR, but that gives an idea of how shockingly fast CRISPR went from strange to news to standard, and how low expectations for genetic engineering were pre-2015 after decades of agonizingly slow progress & high-profile failures & deaths, such that the default assumption was that direct cheap safe genetic engineering of embryos would not be feasible for decades and certainly not the foreseeable future.)
The CRISPR/Cas system exploits a bacterial anti-viral immune system in which snippets of virus DNA are stored and an enzyme system detects the presence in the bacterial genome of fresh viral DNA and then edits it, breaking it, and presumably stopping the infection in its latent phase. This requires the CRISPR enzymes to be highly precise (lest it attack legitimate DNA, damaging or killing itself), repeatable (it’s a poor immune system that can only fight off one infection ever), and programmable by short RNA sequences (because viruses constantly mutate).
This turns out to be usable in animal and human cells to delete/knock-out genes: create an RNA sequence matching a particular gene, inject the RNA sequence along with the key enzymes into a cell, and it will find the gene in question inside the nucleus and snip it; this can be augmented to edit rather than delete by providing another DNA template which the snip-repair mechanisms will unwittingly copy from. Compared to the major earlier approaches using zinc finger nuclease & TALENs, CRISPR is far faster and easier and cheaper to use, with large (at least halving) decreases in time & money cited, and use of it has exploded in research labs, drawing comparisons to the invention of PCR and Nobel Prize predictions. It has been used to edit at least 36 creatures as of June 20157, including:
rhesus monkey embryos ( et al 2017)
sheep
muscly beagles ( et al 2015)
muscly ( et al 2014) & hairy goats ( et al 2015)
human embryos, curing β-thalassaemia ( et al 20158)
curing retinitis pigmentosa in mice cells ( et al 2016) & live mice ( et al 2017) and human cells, ( et al 2016); prelude to planned 2017 trials on Leber congenital amaurosis in live humans and Duchenne muscular dystrophy ( et al 2014)
cure rats or mice of tyrosinemia ( et al 2015, et al 2016), cataracts ( et al 2013), hemophilia, & HIV ( et al 2017)
cure human cells of cystic fibrosis ( et al 2013) and HIV ( et al 2013, et al 2016)
cut out up to 62 copies of the dangerous viral PERV genes from a pig ( et al 2016, et al 2017), with another demonstration in 2019 of ~2.6k edits in a single cell (“Enabling large-scale genome editing by reducing DNA nicking”, et al 2019); other multiple-edit capabilities have been demonstrated; eg. in bacteria ( et al 2014), mice ( et al 2013), rats ( et al 2013), goats ( et al 2015), up to 14 in elephant cells9, and human cells ( et al 2014, et al 2013)
create gene drives in yeast ( et al 2015), fruit flies (2015), & mosquitoes ( et al 2015. et al 2015)
virus-resistant pigs ( et al 2016)
sterile farmed catfish10
cattle with no female offspring which need to be culled11 and vice-versa, chickens without male offspring12
cattle without horns that need to be painfully cut off13
tuberculosis-resistant cows ( et al 2017)
edited ferrets ( et al 2015); ferrets may be used for flu experiments14
autistic-like macaque monkeys ( et al 2016)
planned: make allergen-free eggs15, disease/parasite-resistant bees16, cattle resistant to sleeping sickness17, koi carp of different sizes & color patterns18
(I am convinced some of these were done primarily for the lulz.)
It has appeared to be a very effective and promising genome editing tool in mammalian cells et al 2013 “Targeted genome engineering in human cells with the Cas9 RNA-guided end” http://www.bmskorea.co.kr/bms_email/email201313ya/13-0802/paper.pdf human cells et al 2013 “Multiplex genome engineering using CRISPR/Cas systems” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3795411/ mouse and human cells et al 2012 “A programmable dual-RNA-guided DNA endonuclease in adaptive bacterial immunity” zebrafish somatic cells at the organismal level et al 2013”Efficient genome editing in zebrafish using a CRISPR-Cas system” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3686313/ genomic editing in cultured mammalian cells et al 2013 pluripotent stem cells, but also in zebrafish embryos with efficiencies that are comparable to those obtained using ZFNs and TALENs ( et al 2013).
et al 2016, “Potential of promotion of alleles by genome editing to improve quantitative traits in livestock breeding programs” https://gsejournal.biomedcentral.com/articles/10.1186/s12711-015-0135-3
“Extensive Mammalian Germline Genome Engineering”, et al 2019 (media—“engineering 18 different loci using multiple genome engineering methods” in pigs; followup to et al 2017)
Estimating the profit from CRISPR edits is, in some ways, less straightforward than from embryo selection:
taking the highest n reported betas/coefficients from a GWAS OLS regressions implies that they will be systematically biased upwards due to the winner’s curse and statistical-significance filtering, thereby exaggerating the potential benefit from each SNP
the causal tagging problem: GWAS estimates correlating SNPs with phenotype traits, while valid for prediction (and hence selection), are not necessarily causal (such that an edit at that SNP will have the estimated effect), and the probability of being non-causal
each CRISPR edit has a chance of not making the correct edit, and making wrong edits; an edit may not work in an embryo (the specificity, false negative), and there is a chance of an ‘off-target’ mutation (false positive). A non-edit is a waste of money, while an off-target mutation could be fatal.
CRISPR has advanced at such a rapid rate that numbers on cost, specificity, & off-target mutation rate are generally either not available, or are arguably out of date before they were published19
The winner’s curse can be dealt with several ways; the supplementary of et al 2014 discusses 4 methods (“inverting the conditional expectation of the OLS estimator, maximum likelihood estimation (MLE), Bayesian estimation, and empirical-Bayes estimation”). The best one for our purposes would be a Bayesian approach, yielding posterior distributions of effect sizes. Unfortunately, the raw data for GWAS studies like et al 2013 is not available; but for our purposes, we can, like in the et al 2014 supplement, simply simulate a dataset and work with that to get posteriors to find the SNPs with unbiased largest posterior means.
The causal tagging problem is more difficult. The background for the causal tagging problem is that genes are recombined randomly at conception, but they are not recombined at the individual gene level; rather, genes tend to live in ‘blocks’ of contiguous genes called haplotypes, leading to linkage disequilibrium (LD). Not every possible variant in a haplotype is detected by a SNP array chip, so if you have genes A/B/C/D, it may be the case that a variant of A will increase intelligence but your SNP array chip only detects variants of D; when you do a GWAS, you then discover D predicts increased intelligence. (And if your SNP array chip tags B or C, you may get hits on those as well!) This is not a problem for embryo selection, because if you can only see D’s variants, and you see that an embryo has the ‘good’ D variant, and you pick that embryo, it will indeed grow up as you hoped because that D variant pulled the true causal A variant along for the ride. Indeed, for selection or prediction, the causal tagging problem can be seen as a good thing: your GWASes can pick up effects from parts of the genome you didn’t even pay to sequence - “buy one, get one free”. (The downside can be underestimation due to imperfect proxies.) But this is a problem for embryo editing because if a CRISPR enzyme goes in and carefully edits D while leaving everything untouched, A by definition remains the same and there will be no benefits. A SNP being non-causal is not a serious problem for embryo editing if we know which SNPs are non-causal; as illustrated above, the distribution of effects is smooth enough that discarding a top SNP for the next best alternative costs little. But it is a serious problem if we don’t know which ones are non-causal, because then we waste precious edits (imagine a budget of 30 edits and a non-causal rate of 50%; if we are ignorant which are non-causal, we effectively get only 15 edits, but if we know which to drop, then it’s almost as good as if all were causal). Causality can be established in a few ways; for example, a hit can be reused in a mutant laboratory animal breed to see if it also predicts there (This is behind some striking breakthroughs like et al 2016’s proof that neural pruning is a cause of schizophrenia), either using existing strains or creating a fresh modification (using, say, CRISPR). This has not been done for the top intelligence hits and given the expense & difficulty of animal experimentation, we can’t expect it anytime soon. One can also try to use prior information to boost the posterior probability of an effect: if a gene has already been linked to the nervous system by previous studies exploring mutations or gene expression data etc., or other aspects of the physical structure point towards that SNP like being closest to a gene, then that is evidence for the association being causal. Intelligence hits are enriched for nervous system connections, but this method is inherently weak. A better method is fine-mapping or whole-genome sequencing: when all the variants in a haplotype are sequenced, then the true causal variant will tend to perform subtly better and one can single it out of the whole SNP set using various statistical criteria (eg. et al 2015 using their algorithm on autoimmune disorder estimate 5.5% of their 4.9k SNPs are causal). Useful, but whole-genomes are still expensive enough that they are not created nearly as much as SNPs and there do not seem to be many comparisons to ground-truths or meta-analyses. Another approach is similar to the lab animal approach: human groups differ genetically, and their haplotypes & LD patterns can differ greatly; if D looks associated with intelligence in one group, but is not associated in a genetically distant group with different haplotypes, that strongly suggests that in the first group, D was indeed just proxying for another variant. We can also expect that variants with high frequencies will not be population-specific but be ancient & shared causal variants. Some of the intelligence hits have replicated in European-American samples, as expected but not helpfully; more importantly, in African-American ( et al 2015) and East Asian samples ( et al 2015), and the top SNPs have some predictive power of mean IQs across ethnic groups (2015). More generally, while GWASes usually are paranoid about ancestry, using as homogenous a sample as possible and controlling away any detectable differences in ancestry, GWASes can use cross-ethnic and differing ancestries in “admixture mapping” to home in on causal variants, but this hasn’t been done for intelligence. We can note that some GWASes have compared how hits replicate across populations (eg. et al 2010, et al 2010, et al 2011, et al 2011, et al 2011, et al 2012, et al 2013/ et al 2013, et al 2013, et al 2014, DIAGRAM et al 2014, et al 2015, et al 2015, et al 2015); despite interpretative difficulties such as statistical power, hits often replicate from European-descent samples to distant ethnicities, and the example of the schizophrenia GWASes ( et al 2013, et al 2014) also offers hope in showing a strong correlation of 0.66/0.61 between African & European schizophrenia SNP-based GCTAs. (It also seems to me that there is a trend with the complex highly polygenic traits having better cross-ethnic replicability than in simpler diseases.)
et al 2012, “Consistency of genome-wide associations across major ancestral groups” /doc/genetics/heritable/correlation/2012-ntzani.pdf
2013 “High Trans-ethnic Replicability of GWAS Results Implies Common Causal Variants” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3681663/
“Genetic effects influencing risk for major depressive disorder in China and Europe”, et al 2017 https://www.nature.com/tp/journal/v7/n3/full/tp2016292a.html
“Father Absence and Accelerated Reproductive Development”, et al 2017 https://www.biorxiv.org/content/biorxiv/early/2017/04/04/123711.full.pdf
“Transethnic differences in GWAS signals: A simulation study”, 2018
“Transethnic genetic correlation estimates from summary statistics”, et al 2016
“Molecular Genetic Evidence for Genetic Overlap between General Cognitive Ability and Risk for Schizophrenia: A Report from the Cognitive Genomics Consortium (COGENT)”, et al 2013/2014: IQ PGS applied to schizophrenia case status:
EA: 0.41%
Japanese: 0.38%
Ashkenazi Jew: 0.16%
MGS African-American: 0.00%
myopia (refractive error): European/East Asian ( et al 2018, “Genome-wide association meta-analysis highlights light-induced signaling as a driver for refractive error”): r_g = 0.90/0.80
“Consistent Association of Type 2 Diabetes Risk Variants Found in Europeans in Diverse Racial and Ethnic Groups”, et al 2010 https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1001078 et al 2017, “Heterogeneity in polygenic scores for common human traits” https://www.biorxiv.org/content/early/2017/02/05/106062.full Figure 3 - the height/education/etc polygenic scores roughly 5x as predictive in white Americans as African-Americans, ~0.05 R^2 vs ~0.01 R^2, and since African-Americans average about 25% white anyway, that’s consistent with 10% or less… “Using Genetic Distance to Infer the Accuracy of Genomic Prediction”, et al 2016 https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1006288
Height PGSes don’t work crossracially: “Human Demographic History Impacts Genetic Risk Prediction across Diverse Populations”, et al 2017 (note that this paper had errors considerably exaggerating the decline):
The vast majority of genome-wide association studies (GWASs) are performed in Europeans, and their transferability to other populations is dependent on many factors (eg. linkage disequilibrium, allele frequencies, genetic architecture). As medical genomics studies become increasingly large and diverse, gaining insights into population history and consequently the transferability of disease risk measurement is critical. Here, we disentangle recent population history in the widely used 1000 Genomes Project reference panel, with an emphasis on populations underrepresented in medical studies. To examine the transferability of single-ancestry GWASs, we used published summary statistics to calculate polygenic risk scores for eight well-studied phenotypes. We identify directional inconsistencies in all scores; for example, height is predicted to decrease with genetic distance from Europeans, despite robust anthropological evidence that West Africans are as tall as Europeans on average. To gain deeper quantitative insights into GWAS transferability, we developed a complex trait coalescent-based simulation framework considering effects of polygenicity, causal allele frequency divergence, and heritability. As expected, correlations between true and inferred risk are typically highest in the population from which summary statistics were derived. We demonstrate that scores inferred from European GWASs are biased by genetic drift in other populations even when choosing the same causal variants and that biases in any direction are possible and unpredictable. This work cautions that summarizing findings from large-scale GWASs may have limited portability to other populations using standard approaches and highlights the need for generalized risk prediction methods and the inclusion of more diverse individuals in medical genomics.
“Genetic contributors to variation in alcohol consumption vary by race/ethnicity in a large multi-ethnic genome-wide association study”, et al 2017 /doc/genetics/heritable/correlation/2017-jorgenson.pdf
“High-Resolution Genetic Maps Identify Multiple Type 2 Diabetes Loci at Regulatory Hotspots in African Americans and Europeans”, et al 2017 /doc/genetics/heritable/correlation/2017-lau.pdf
“The genomic landscape of African populations in health and disease”, et al 2017 /doc/genetics/selection/2017-rotimi.pdf
Wray et al (MDDWG PGC) 2017, “Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression”:
European/Chinese depression: rg = 0.31
European/Chinese schizophrenia: rg = 0.34
European/Chinese bipolar disorder: rg = 0.45
“Genetic Diversity Turns a New PAGE in Our Understanding of Complex Traits”, et al 2017:
To demonstrate the benefit of studying underrepresented populations, the Population Architecture using Genomics and Epidemiology (PAGE) study conducted a GWAS of 26 clinical and behavioral phenotypes in 49,839 non-European individuals. Using novel strategies for multi-ethnic analysis of admixed populations, we confirm 574 GWAS catalog variants across these traits, and find 28 novel loci and 42 residual signals in known loci. Our data show strong evidence of effect-size heterogeneity across ancestries for published GWAS associations, which substantially restricts genetically-guided precision medicine. We advocate for new, large genome-wide efforts in diverse populations to reduce health disparities.
et al 2017, “Genome-wide association study identifies 112 new loci for body mass index in the Japanese population”: r = 0.82 between top European/Japanese SNP hits
“Generalizing Genetic Risk Scores from Europeans to Hispanics/Latinos”, et al 2018:
…we compare various approaches for GRS construction, using GWAS results from both large EA studies and a smaller study in Hispanics/Latinos, the Hispanic Community Health Study/Study of Latinos (HCHS/SOL, n=12,803). We consider multiple ways to select SNPs from association regions and to calculate the SNP weights. We study the performance of the resulting GRSs in an independent study of Hispanics/Latinos from the Woman Health Initiative (WHI, n=3,582). We support our investigation with simulation studies of potential genetic architectures in a single locus. We observed that selecting variants based on EA GWASs generally performs well, as long as SNP weights are calculated using Hispanics/Latinos GWASs, or using the meta-analysis of EA and Hispanics/Latinos GWASs. The optimal approach depends on the genetic architecture of the trait.
“Genetic architecture of gene expression traits across diverse populations”, et al 2018: causal variants are mostly shared cross-racially despite different LD patterns, as indicated by similar gene expression effects?
Consistent with the concordant direction of effect at associated SNPs, there was high genetic correlation (rG) between the European and East Asian cohort when considering the additive effects of all SNPs genotyped on the Immunochip19 (Crohn’s disease rG = 0.76, ulcerative colitis rG = 0.79) (Supplementary Table 11). Given that rare SNPs (minor allele frequency (MAF) < 1%) are more likely to be population-specific, these high rG values also support the notion that the majority of causal variants are common (MAF>5%).
“Theoretical and empirical quantification of the accuracy of polygenic scores in ancestry divergent populations”, et al 2020:
Polygenic scores (PGS) have been widely used to predict complex traits and risk of diseases using variants identified from genome-wide association studies (GWASs). To date, most GWASs have been conducted in populations of European ancestry, which limits the use of GWAS-derived PGS in non-European populations. Here, we develop a new theory to predict the relative accuracy (RA, relative to the accuracy in populations of the same ancestry as the discovery population) of PGS across ancestries. We used simulations and real data from the UK Biobank to evaluate our results. We found across various simulation scenarios that the RA of PGS based on trait-associated SNPs can be predicted accurately from modeling linkage disequilibrium (LD), minor allele frequencies (MAF), cross-population correlations of SNP effect sizes and heritability. Altogether, we find that LD and MAF differences between ancestries explain alone up to ~70% of the loss of RA using European-based PGS in African ancestry for traits like body mass index and height. Our results suggest that causal variants underlying common genetic variation identified in European ancestry GWASs are mostly shared across continents.
“Polygenic prediction of the phenome, across ancestry, in emerging adulthood”, et al 2017 (supplement): large loss of PGS power in many traits, but direct comparison seems to be unavailable for most of the PGSes other than stuff like height?
“Genetics of self-reported risk-taking behavior, trans-ethnic consistency and relevance to brain gene expression”, et al 2018:
There were strong positive genetic correlations between risk-taking and attention-deficit hyperactivity disorder, bipolar disorder and schizophrenia. Index genetic variants demonstrated effects generally consistent with the discovery analysis in individuals of non-British White, South Asian, African-Caribbean or mixed ethnicity.
Polygenic risk scores are gaining more and more attention for estimating genetic risks for liabilities, especially for noncommunicable diseases. They are now calculated using thousands of DNA markers. In this paper, we compare the score distributions of two previously published very large risk score models within different populations. We show that the risk score model together with its risk stratification thresholds, built upon the data of one population, cannot be applied to another population without taking into account the target population’s structure. We also show that if an individual is classified to the wrong population, his/her disease risk can be systematically incorrectly estimated.
“Analysis of Polygenic Score Usage and Performance across Diverse Human Populations”, et al 2018:
We analyzed the first decade of polygenic scoring studies (2008–2017, inclusive), and found that 67% of studies included exclusively European ancestry participants and another 19% included only East Asian ancestry participants. Only 3.8% of studies were carried out on samples of African, Hispanic, or Indigenous peoples. We find that effect sizes for European ancestry-derived polygenic scores are only 36% as large in African ancestry samples, as in European ancestry samples (t=-10.056, df=22, p=5.5x10-10). Poorer performance was also observed in other non-European ancestry samples. Analysis of polygenic scores in the 1000Genomes samples revealed many strong correlations with global principal components, and relationships between height polygenic scores and height phenotypes that were highly variable depending on methodological choices in polygenic score construction.
“Transancestral GWAS of alcohol dependence reveals common genetic underpinnings with psychiatric disorders”, et al 2018:
PRS based on our meta-analysis of AD were significantly predictive of AD outcomes in all three tested external cohorts. PRS derived from the unrelated EU GWAS predicted up to 0.51% of the variance in past month alcohol use disorder in the Avon Longitudinal Study of Parents and Children (ALSPAC; P=0.0195; Supplementary Fig. 10a) and up to 0.3% of problem drinking in Generation Scotland (P=7.9×10-6; Supplementary Fig. 10b) as indexed by the CAGE (Cutting down, Annoyance by criticism, Guilty feelings, and Eye-openers) questionnaire. PRS derived from the unrelated AA GWAS predicted up to 1.7% of the variance in alcohol dependence in the COGA AAfGWAS cohort (P=1.92×10-7; Supplementary Fig. 10c). Notably, PRS derived from the unrelated EU GWAS showed much weaker prediction (maximum r2=0.37%, P=0.01; Supplementary Fig. 10d) in the COGA AAfGWAS than the ancestrally matched AA GWAS-based PRS despite the much smaller discovery sample for AA. In addition, the AA GWAS-based AD PRS also still yielded significant variance explained after controlling for other genetic factors (r2=1.16%, P=2.5×10-7). Prediction of CAGE scores in Generation Scotland remained significant and showed minimal attenuation (r2=0.29%, P=1.0×10-5) after conditioning on PRS for alcohol consumption derived from UK Biobank results17. In COGA AAfGWAS, the AA PRS derived from our study continued to predict 1.6% of the variance in alcohol dependence after inclusion of rs2066702 genotype as a covariate, indicating independent polygenic effects beyond the lead ADH1B variant (Supplementary Methods).
So EU->AA PGS is 0.37/1.7=21%?
“The transferability of lipid-associated loci across African, Asian and European cohorts”, et al 2019:
A polygenic score based on established LDL-cholesterol-associated loci from European discovery samples had consistent effects on serum levels in samples from the UK, Uganda and Greek population isolates (correlation coefficient r=0.23 to 0.28 per LDL standard deviation, p<1.9x10-14). Trans-ethnic genetic correlations between European ancestry, Chinese and Japanese cohorts did not differ significantly from 1 for HDL, LDL and triglycerides. In each study, >60% of major lipid loci displayed evidence of replication with one exception. There was evidence for an effect on serum levels in the Ugandan samples for only 10% of major triglyceride loci. The PRS was only weakly associated in this group (r=0.06, SE=0.013).
“Identification of 28 new susceptibility loci for type 2 diabetes in the Japanese population”, et al 2019:
When we compared the effect sizes of 69 of the 88 lead variants in Japanese and Europeans that were available in a published European GWAS2 (Supplementary Table 3 and Supplementary Fig. 5), we found a strong positive correlation (Pearson’s r = 0.87, p = 1.4 × 10−22) and directional consistency (65 of 69 loci, 94%, sign-test p = 3.1 × 10−15). In addition, when we compared the effect sizes of the 95 of 113 lead variants reported in the European type 2 diabetes GWAS2 that were available in both Japanese and European type 2 diabetes GWAS (Supplementary Table 2 and Supplementary Fig. 6a), we also found a strong positive correlation (Pearson’s r = 0.74, p = 5.9 × 10−18) and directional consistency (83 of 95 loci, 87%, sign-test p = 3.2 × 10−14). After this manuscript was submitted, a larger type 2 diabetes GWAS of European ancestry was published17. When we repeated the comparison at the lead variants reported in this larger European GWAS, we found a more prominent correlation (Pearson’s r = 0.83, p = 8.7 × 10−51) and directional consistency (181 of 192 loci, 94%, sign-test p = 8.3 × 10−41) of the effect sizes (Supplementary Table 4 and Supplementary Fig. 6b). These results indicate that most of the type 2 diabetes susceptibility loci identified in the Japanese or European population had comparable effects on type 2 diabetes in the other population.
“Identification of type 2 diabetes loci in 433,540 East Asian individuals”, et al 2019:
Overall, the per-allele effect sizes between the two ancestries were moderately correlated (r=0.54; Figure 2A). When the comparison was restricted to the 290 variants that are common (MAF≥5%) in both ancestries, the effect size correlation increased to r=0.71 (Figure 2B; Supplementary Figure 8). This effect size correlation further increased to r=0.88 for 116 variants significantly associated with T2D (P<5x10-8) in both ancestries. While the overall effect sizes for all 343 variants appear, on average, to be stronger in East Asian individuals than European, this trend is reduced when each locus is represented only by the lead variant from one population (Supplementary Figure 9). Specifically, many variants identified with larger effect sizes in the European meta-analysis are missing from the comparison because they were rare/monomorphic or poorly imputed in the East Asian meta-analysis, for which imputation reference panels are less comprehensive compared to the European-centric Haplotype Reference Consortium panel.
“Genetic analyses of diverse populations improves discovery for complex traits”, Wojcik
When stratified by self-identified race/ethnicity, the effect sizes for the Hispanic/Latino population remained significantly attenuated compared to the previously reported effect sizes (β= 0.86; 95% confidence interval = 0.83–0.90; Fig. 2a). Effect sizes for the African American population were even further diminished at nearly half the strength (β= 0.54; 95% confidence interval = 0.50–0.58; Fig. 2a). This is suggestive of truly differential effect sizes between ancestries at previously reported variants, rather than these effect sizes being upwardly biased in general (that is, exhibiting ‘winner’s curse’), which should affect all groups equally.
“Contributions of common genetic variants to risk of schizophrenia among individuals of African and Latino ancestry”, et al 2019:
Consistent with previous reports demonstrating the generalizability of polygenic findings for schizophrenia across diverse populations [14, 43, 44], individual-level scores constructed from PGC-SCZ2 summary statistics were significantly associated with case−control status in admixed African, Latino, and European cohorts in the current study (Fig. 2a). When considering scores constructed from approximately independent common variants (pairwise r2 < 0.1), we observed the best overall prediction at a P value threshold (PT) of 0.05; these scores explained ~3.5% of the variance in schizophrenia liability among Europeans (P = 4.03 × 10−110), ~1.7% among Latino individuals (P = 9.02 × 10−52), and ~0.5% among admixed African individuals (P = 8.25 × 10−19) (Fig. 2a; Supplemental Table 6). Consistent with expectation, when comparing results for scores constructed from larger numbers of nonindependent SNPs, we generally observed an improvement in predictive value (Fig. 2b; Supplemental Table 7).
Polygenic scores based on African ancestry GWAS results were significantly associated with schizophrenia among admixed African individuals, attaining the best overall predictive value when constructed from approximately independent common variants (pairwise r2 < 0.1) with PT ≤ 0.5 in the discovery analysis (Fig. 2a and Supplemental Table 6); this score explained ~1.3% of the variance in schizophrenia liability (P = 3.47 × 10−41). Scores trained on African ancestry GWAS results also significantly predicted case−control status across populations; scores based on a PT ≤ 0.5 and pairwise r2 < 0.8 explained ~0.2% of the variability in liability in Europeans (P = 2.35 × 10−7) and ~0.1% among Latino individuals (P = 0.000184) (Fig. 2b and Supplemental Table 7). Similarly, scores constructed from Latino GWAS results (PT ≤ 0.5) were of greatest predictive value among Latinos (liability R2 = 2%; P = 3.11 × 10−19) and Europeans (liability R2 = 0.8%; P = 1.60 × 10−9); with scores based on PT ≤ 0.05 and pairwise r2 < 0.1 showing nominally significant association with case-control status among African ancestry individuals (liability R2 = 0.2%; P = 0.00513).
We next considered polygenic scores constructed from trans-ancestry meta-analysis of PGC-SCZ2 summary statistics and our African and Latino GWAS, which revealed increased significance and improved predictive value in all three ancestries. Among African ancestry individuals, meta-analytic scores based on PT ≤ 0.5 explained ~1.7% of the variance (P = 4.37 × 10−53); while scores based on PT ≤ 0.05 accounted for ~2.1% and ~3.7% of the variability in liability among Latino (P = 1.10 × 10−59) and European individuals (P = 1.73 × 10−114), respectively.
“Quantifying genetic heterogeneity between continental populations for human height and body mass index”, et al 2019:
Genome-wide association studies (GWAS) in samples of European ancestry have identified thousands of genetic variants associated with complex traits in humans. However, it remains largely unclear whether these associations can be used in non-European populations. Here, we seek to quantify the proportion of genetic variation for a complex trait shared between continental populations. We estimated the between-population correlation of genetic effects at all SNPs (rg) or genome-wide significant SNPs (rg(GWS)) for height and body mass index (BMI) in samples of European (EUR; n = 49,839) and African (AFR; n = 17,426) ancestry. The rg between EUR and AFR was 0.75 (s. e. = 0.035) for height and 0.68 (s. e. = 0.062) for BMI, and the corresponding rg(gwas) was 0.82 (s. e. = 0.030) for height and 0.87 (s. e. = 0.064) for BMI, suggesting that a large proportion of GWAS findings discovered in Europeans are likely applicable to non-Europeans for height and BMI. There was no evidence that rg differs in SNP groups with different levels of between-population difference in allele frequency or linkage disequilibrium, which, however, can be due to the lack of power.
To elucidate the genetics of coronary artery disease (CAD) in the Japanese population, we conducted a large-scale genome-wide association study (GWAS) of 168,228 Japanese (25,892 cases and 142,336 controls) with genotype imputation using a newly developed reference panel of Japanese haplotypes including 1,782 CAD cases and 3,148 controls. We detected 9 novel disease-susceptibility loci and Japanese-specific rare variants contributing to disease severity and increased cardiovascular mortality. We then conducted a transethnic meta-analysis and discovered 37 additional novel loci. Using the result of the meta-analysis, we derived a polygenic risk score (PRS) for CAD, which outperformed those derived from either Japanese or European GWAS. The PRS prioritized risk factors among various clinical parameters and segregated individuals with increased risk of long-term cardiovascular mortality. Our data improves clinical characterization of CAD genetics and suggests the utility of transethnic meta-analysis for PRS derivation in non-European populations.
“Genetic Risk Scores for Cardiometabolic Traits in Sub-Saharan African Populations”, et al 2020:
There is growing support for the use of genetic risk scores (GRS) in routine clinical settings. Due to the limited diversity of current genomic discovery samples, there are concerns that the predictive power of GRS will be limited in non-European ancestry populations. Here, we evaluated the predictive utility of GRS for 12 cardiometabolic traits in sub-Saharan Africans (AF; n=5200), African Americans (AA; n=9139), and European Americans (EA; n=9594). GRS were constructed as weighted sums of the number of risk alleles. Predictive utility was assessed using the additional phenotypic variance explained and increase in discriminatory ability over traditional risk factors (age, sex and BMI), with adjustment for ancestry-derived principal components. Across all traits, GRS showed upto a 5-fold and 20-fold greater predictive utility in EA relative to AA and AF, respectively. Predictive utility was most consistent for lipid traits, with percent increase in explained variation attributable to GRS ranging from 10.6% to 127.1% among EA, 26.6% to 65.8% among AA, and 2.4% to 37.5% among AF. These differences were recapitulated in the discriminatory power, whereby the predictive utility of GRS was 4-fold greater in EA relative to AA and up to 44-fold greater in EA relative to AF. Obesity and blood pressure traits showed a similar pattern of greater predictive utility among EA.
Given the practice of embryo editing, the causal tagging problem can gradually solve itself: as edits are made, forcibly breaking the potential confounds, the causal nature of an SNP becomes clear. But how to allocate edits across the top SNPs to determine each’s causal nature as efficiently as possible without spending too many edits investigating? A naive answer might be something along the lines of a power analysis: in a two-group t-test trying to detect a difference of ~0.03 SD for each variant (the rough size of the top few variants), with variance reduced by the known polygenic score, and desired power is the standard 80%; it follows that one would need to randomize a total sample of n = 34842 to reject the null hypothesis of 0 effect20. Setting up a factorial experiment & randomizing several variants simultaneously may allow inferences on them as well, but clearly this is going to be a tough row to hoe. This is unduly pessimistic, since we neither need nor desire 80% power, nor are we comparing to a null hypothesis, as our goal is more modest: since only a certain number of edits will be doable for any embryo, say 30, we merely want to accumulate enough evidence about the top 30 variants to either demote it to #31 (and so we no longer spend any edits on it) or confirm it belongs in the top 30 and we should always be editing it. This is immediately recognizable as reinforcement learning: the multi-armed bandit (MAB) problem (each possible edit being an independent arm which can pulled or not); or more precisely, since early childhood (5yo) IQ scores are relatively poorly correlated with adult scores (r = 0.55) and many embryos may be edited before data on the first edits starts coming in, a multi-armed bandit with multiple plays and delayed feedback. (There is no way immediately upon birth to receive meaningful feedback about the effect of an edit, although there might be ways to get feedback faster, such as using short-sleeper gene edits to enhance education.) Thompson sampling is a randomized Bayesian approach which is simple and theoretically optimal, with excellent performance in practice as well; an extension to multiple plays is also optimal. Dealing with the delayed feedback is known to be difficult and multiple-play Thompson sampling may not be optimal, but in simulations it performs better with delayed feedback than other standard MABs. We can consider a simulation of the scenario in which every time-step is a day and 1 or more embryos must be edited that day; a noisy measure of IQ is then made available 9*31+5*365=2104 days later, which is fed into a GWAS mixture model in which the GWAS correlation for each SNP is considered as drawn with an unknown probability from a causal distribution and from a nuisance distribution, so with additional data, the effect estimates of the SNPs are refined, the probability of being drawn from the causal distribution is refined, and the overall mixture probability is likewise refined, similar to the “Bayes B” paradigm from the “Bayesian alphabet” of genomic prediction methods in animal breeding. (So for the first 2104 time-steps, a Thompson sample would be performed to yield a new set of edits, then each subsequent time-step a datapoint would mature, the posteriors updated, and another set of edits created.) The relevant question is how much regret will fall and how many causal SNPs become the top picks after how many edits & days: hopefully high performance & low regret will be achieved within a few years after the initial 5-year delay.
a more concrete example: imagine we have a budget of 60 edits (based on the multiplex pig editing), a causal probability of 10%, an exponential distribution (rate 70.87) over 500000 candidate alleles of which we consider the top 1000, each of which has a frequency of 50% and we sequence before editing to avoid wasting edits. What is our best case and worst-case IQ increase? In the worst case, the top 60 are all non-causal, so our improvement is 0 IQ points; in the best case where all hits are causal, half of the hits are discarded after sequencing, and then the remaining top 60 get us ~6.1 IQ points; the intermediate case of 10% causal gets us to ~0.61 IQ points, and so our regret is 5.49 IQ points per embryo. Unsurprisingly, a 10% causal rate is horribly inefficient. In the 10% case, if we can infer the true causal SNPs, we only need to start with ~600 SNPs to saturate our editing budget on average, or ~900 to have <1% chance of winding up with <60 causal SNPs, so 1000 SNPs seems like a good starting point. (Of course, we also want a larger window so as our edit budget increases with future income growth & technological improvement, we can smoothly incorporate the additional SNPs.) So what order of samples do we need here to reduce our regret of 5.49 to something more reasonable like <0.25 IQ points?
SNPs <- 500000
SNPlimit <- 1000
rate <- 70.87
editBudget <- 60
frequency <- 0.5
mean(replicate(1000, {
hits <- sort(rexp(SNPs, rate=rate), decreasing=TRUE)[1:SNPlimit]
sum(sample(hits, length(hits) * 0.5)[1:editBudget])
}))http://jmlr.csail.mit.edu/proceedings/papers/v31/agrawal13a.pdf Regret of Thompson sampling with Gaussian priors & likelihood is O(sqrt(N * T * ln(N))), where N = number of different arms/actions and T = current timestep hence, if we have 1000 actions and we sample 1 time, our expected total regret is on the order of sqrt(1000 * 1 * ln(1000)) = 83; with 100 samples, our expected total regret has increased by two orders to 831 but we are only incurring an additional expected regret of ~4 or 5% of the first timestep’s regret diff(sapply((1:10000, function(t) { sqrt(1000 * t * log(1000)) } )))
Thompson sampling also achieves the lower bound in multiple-play but the asymptotic is more complex, and does not take into account the long delay & noise in measuring IQ. TS empirically performs well but hard to know what sort of sample size is required. But at least we can say that the asymptotics don’t imply dozens of thousands of embryos.
problem: what’s the probability of non-causal tagging due to LD? probably low since they work cross-ethnically don’t they? on the other hand: https://emilkirkegaard.dk/en/?p=5415 > “If the GWAS SNPs owe their predictive power to being actual causal variants, then LD is irrelevant and they should predict the relevant outcome in any racial group. If however they owe wholly or partly their predictive power to just being statistically related to causal variants, they should be relatively worse predictors in racial groups that are most distantly related. One can investigate this by comparing the predictive power of GWAS betas derived from one population on another population. Since there are by now 1000s of GWAS, meta-analyses have in fact made such comparisons, mostly for disease traits. Two reviews found substantial cross-validity for the Eurasian population (Europeans and East Asians), and less for Africans (usually African Americans) (23,24). The first review only relied on SNPs with p < α and found weaker results. This is expected because using only these is a threshold effect, as discussed earlier.
The second review (from 201313ya; 299 included GWAS) found much stronger results, probably because it included more SNPs and because they also adjusted for statistical power. Doing so, they found that: ~100% of SNPs replicate in other European samples when accounting for statistical power, ~80% in East Asian samples but only ~10% in the African American sample (not adjusted for statistical power, which was ~60% on average). There were fairly few GWAS for AAs however, so some caution is needed in interpreting the number. Still, this throws some doubt on the usefulness of GWAS results from Europeans or Asians used on African samples (or reversely).” and https://emilkirkegaard.dk/en/?p=6415
“Identifying Causal Variants at Loci with Multiple Signals of Association”, et al 2014 http://genetics.org/content/198/2/497.full “Where is the causal variant? On the advantage of the family design over the case-control design in genetic association studies”, Dandine-2015 https://www.nature.com/ejhg/journal/v23/n10/abs/ejhg2014284a.html worst-case, ~10% of SNPs are causal?
https://www.addgene.org/crispr/reference/ https://www.genome.gov/about-genomics/fact-sheets/Sequencing-Human-Genome-cost https://crispr.bme.gatech.edu/ http://crispr.mit.edu/ low, near zero mutation rates: “High-fidelity CRISPR-Cas9 nucleases with no detectable genome-wide off-target effects” et al 2016, /doc/genetics/editing/2016-kleinstiver.pdf ; “Rationally engineered Cas9 nucleases with improved specificity”, et al 2016 /doc/genetics/editing/2016-slaymaker.pdf Church, April 2016: “Indeed, the latest versions of gene-editing enzymes have zero detectable off-target activities.” https://www.wsj.com/articles/should-heritable-gene-editing-be-used-on-humans-1460340173 Church, June 2016 “Church: In practice, when we introduced our first CRISPR in 201313ya,19 it was about 5% off target. In other words, CRISPR would edit five treated cells out of 100 in the wrong place in the genome. Now, we can get down to about one error per 6 trillion cells…Fahy: Just how efficient is CRISPR at editing targeted genes? Church: Without any particular tricks, you can get anywhere up to, on the high end, into the range of 50% to 80% or more of targeted genes actually getting edited in the intended way. Fahy: Why not 100%? Church: We don’t really know, but over time, we’re getting closer and closer to 100%, and I suspect that someday we will get to 100%. Fahy: Can you get a higher percentage of successful gene edits by dosing with CRISPR more than once? Church: Yes, but there are limits.” http://www.lifeextension.com/Lpages/2016/CRISPR/index “A person familiar with the research says ‘many tens’ of human IVF embryos were created for the experiment using the donated sperm of men carrying inherited disease mutations. Embryos at this stages are tiny clumps of cells invisible to the naked eye. ‘It is proof of principle that it can work. They significantly reduced mosaicism. I don’t think it’s the start of clinical trials yet, but it does take it further than anyone has before’, said a scientist familiar with the project. Mitalipov’s group appears to have overcome earlier difficulties by ‘getting in early’ and injecting CRISPR into the eggs at the same time they were fertilized with sperm.” https://www.technologyreview.com/2017/07/26/68093/first-human-embryos-edited-in-us/ cost of the top variants? want to edit all variants such that: sequencing-based edit: posterior mean * value of IQ point > cost of 1 edit for blind edits: probability of the bad variant * posterior mean * value of IQ point > cost of 1 edit
how to simulate posterior probabilities? https://cran.r-project.org/web/packages/BGLR/BGLR.pdf https://cran.r-project.org/web/packages/BGLR/vignettes/BGLR-extdoc.pdf looks useful but won’t handle the mixture modeling
previous: et al 2015 “CRISPR/Cas9-mediated gene editing in human tripronuclear zygotes” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4417674/ https://www.nature.com/news/chinese-scientists-genetically-modify-human-embryos-1.17378 et al 2016, “Introducing precise genetic modifications into human 3PN embryos by CRISPR/Cas-mediated genome editing” /doc/genetics/editing/2016-kang.pdf https://www.nature.com/news/second-chinese-team-reports-gene-editing-in-human-embryos-1.19718 et al 2016, “Programmable editing of a target base in genomic DNA without double-stranded DNA cleavage” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4873371/ https://www.nature.com/articles/nature.2016.20302 “CRISPR/Cas9-mediated gene editing in human zygotes using Cas9 protein” et al 2017 /doc/genetics/editing/2017-tang.pdf : no observed off-target mutations; efficiency of 20%, 50%, and 100% “Correction of a pathogenic gene mutation in human embryos”, et al 2017 https://www.nature.com/articles/nature23305 no observed off-targets, 27.9% efficiency
legal in USA (no legislation but some interesting regulatory wrinkles: see ch7 of Human Genome Editing: Science, Ethics, and Governance 2017 ), legal in China (only ‘unenforceable guidelines’) as of 201412ya, according to “International regulatory landscape and integration of corrective genome editing into in vitro fertilization”, 2014 http://rbej.biomedcentral.com/articles/10.1186/1477-7827-12-108 as of 201511ya too according to https://www.nature.com/news/where-in-the-world-could-the-first-crispr-baby-be-born-1.18542 loophole closed post-He Jiankui & made definitely illegal: “China officially bans CRISPR babies, human clones and animal-human hybrids” illegal in the UK but they have given permission to modify human embryos for research http://www.popsci.com/scientists-get-government-approval-to-edit-human-embryos? https://www.nytimes.com/2016/02/02/health/crispr-gene-editing-human-embryos-kathy-niakan-britain.html legal in Japan for research, but maybe not application? https://mainichi.jp/english/articles/20160423/p2g/00m/0dm/002000c legal in Sweden for editing, which has been done as of September 2016 by Fredrik Lanner https://www.npr.org/sections/health-shots/2016/09/22/494591738/breaking-taboo-swedish-scientist-seeks-to-edit-dna-of-healthy-human-embryos
Also, what about mosaicism? When the CRISPR RNA is injected into an even single-celled zygote, it may already have created some of the DNA for a split and so the edit covers only a fraction of the cells of the future full-grown organism. “Additionally, editing may happen after first embryonic division, due to persistence of Cas9:gRNA complexes, also causing mosaicism. We (unpublished results) and others ( et al 2013a; et al 2014; et al 2014) have observed mosaic animals carrying three or more alleles. A recent study reported surprisingly high percentage of mosaic mice (up to 80%) generated by CRISPR targeting of the tyrosinase gene (Tyr) (). We have observed a varying frequency of mosaicism, 11-35%, depending on the gene/locus (our unpublished data)… The pronuclear microinjection of gRNA and Cas9, in a manner essentially identical to what is used for generating transgenic mice, can be easily adapted by most transgenic facilities. Facilities equipped with a Piezo-electric micromanipulator can opt for cytoplasmic injections as reported ( et al 2013; ). et al 2014 performed an extensive comparison study suggesting that cytoplasmic injection of a gRNA and Cas9 mRNA mixture as the best delivery method. Although the overall editing efficiency in born pups yielded by pronuclear versus cytoplasmic RNA injection seems to be comparable (Table 1), the latter method generated two- to fourfold more live born pups. Injection of plasmid DNA carrying Cas9 and gRNA to the pronucleus was the least efficient method in terms of survival and targeting efficiency ( et al 2013; et al 2014). Injection into pronuclei seems to be more damaging to embryos than injection of the same volume or concentration of editing reagents to the cytoplasm. It has been shown that cytoplasmic injection of Cas9 mRNA at concentrations up to 200 ng/μl is not toxic to embryos ( et al 2013) and efficient editing was achieved at concentrations as low as 1.5 ng/μl ( et al 2013a). In our hands, injecting Cas9 mRNA at 50-150 ng/μl and gRNA at 50-75 ng/μl first into the pronucleus and also into the cytoplasm as the needle is being withdrawn, yields good survival of embryos and efficient editing by NHEJ in live born pups (our unpublished observations).” http://genetics.org/content/199/1/1.full
dnorm((150-100)/15) * 320000000 [1] 493,529.2788 dnorm((170-100)/15) * 320000000 [1] 2382.734679
if you’re curious how I calculated that, (10*1000 + 10 * 98 * 500) > 500000 → [1] FALSE sum(sort((rexp(10000)/1)/18, decreasing=TRUE)[1:98] * 0.5) → [1] 15.07656556
hm. there are ~50k IVF babies each year in the USA. my quick CRISPR sketch suggested that for a few mill you could get up to 150-170. dnorm((150-100)/15) * 320000000 → [1] 493,529.2788; dnorm((170-100)/15) * 320000000 → [1] 2382.734679. so depending on how many IVFers used it, you could boost the total genius population by anywhere from 1/10th to 9x
but if only 10% causal rate and so only 100 effective edits from 1000, and a net gain of 15 IQ points (1SD) then increases: IVF <- (dnorm((115-100)/15) * 50000); genpop <- (dnorm((150-100)/15) * 320000000); (IVF+genpop)/genpop [1] 1.024514323 IVF <- (dnorm((115-100)/15) * 50000); genpop <- (dnorm((170-100)/15) * 320000000); (IVF+genpop)/genpop [1] 6.077584313 an increase of 1.02x (150) and 6x (170) respectively
“To confirm these GUIDE-seq findings, we used targeted amplicon sequencing to more directly measure the frequencies of indel mutations induced by wild-type SpCas9 and SpCas9-HF1. For these experiments, we transfected human cells only with sgRNA- and Cas9encoding plasmids (without the GUIDE-seq tag). We used next-generation sequencing to examine the on-target sites and 36 of the 40 off-target sites that had been identified for six sgRNAs with wild-type SpCas9 in our GUIDE-seq experiments (four of the 40 sites could not be specifically amplified from genomic DNA). These deep sequencing experiments showed that: (1) wild-type SpCas9 and SpCas9-HF1 induced comparable frequencies of indels at each of the six sgRNA on-target sites, indicating that the nucleases and sgRNAs were functional in all experimental replicates (Fig. 3a, b); (2) as expected, wild-type SpCas9 showed statistically-significant evidence of indel mutations at 35 of the 36 off-target sites (Fig. 3b) at frequencies that correlated well with GUIDE-seq read counts for these same sites (Fig. 3c); and (3) the frequencies of indels induced by SpCas9-HF1 at 34 of the 36 off-target sites were statistically indistinguishable from the background level of indels observed in samples from control transfections (Fig. 3b). For the two off-target sites that appeared to have statistically-significant mutation frequencies with SpCas9-HF1 relative to the negative control, the mean frequencies of indels were 0.049% and 0.037%, levels at which it is difficult to determine whether these are due to sequencing or PCR error or are bona fide nuclease-induced indels. Based on these results, we conclude that SpCas9-HF1 can completely or nearly completely reduce off-target mutations that occur across a range of different frequencies with wild-type SpCas9 to levels generally undetectable by GUIDE-seq and targeted deep sequencing.”
So no detected off-target mutations down to the level of lab error rate detectability. Amazing. So you can do a CRISPR on a cell with a >75% chance of making the edit to a desired gene correctly, and a <0.05% chance of a mistaken (potentially harmless) edit/mutation on a similar gene. With an error rate that low, you could do hundreds of CRISPR edits to a set of embryos with a low net risk of error… The median number of eggs extracted from a woman during IVF in America is ~9; assume the worst case of 0.05% risk of off-target mutation and that one scraps any embryo found to have any mutation at all even if it looks harmless; then the probability of making 1000 edits without an off-target mutation could be (1-(0.05/100)) ^ 1000 = 60%, so you’re left with 5.4 good embryos, which is a decent yield. Making an edit of the top 1000 betas from the 2013 polygenic score and figuring that it’s weakened by maybe 25% due to particular cells not getting particular edits and that is… a very large number.
When I was doing my dysgenics analysis, I found that the Rietveld betas could be reasonably approximated by rexp, and we can anchor it by assuming the biggest effect is 0.5 IQ points, so we divide by 18, in which case we might estimate the top 750 edits at a cumulative value of sum(sort((rexp(10000)/1)/18, decreasing=TRUE)[1:750] * 0.5) → [1] 73.97740467. (Caveats: assumes knowledge of true betas, needs to be weakened for actual posterior probabilities, etc. etc.)
How much did that <74 IQ points cost? Well, I hear that TALENS in bulk costs $500 so you could ballpark marginal costs of particular CRISPR edits at that much too (and hopefully much less), and whole-genomes still cost $1k, and you need to do 1000 edits on each embryo and whole-genomes at the end to check for off-target mutations, so you could ballpark a full suite of edits to 10 embryos at ~$5m: 10*1000 + 10 * 1000 * 500 → [1] 5010000. Of them 40% will have an off-target mutation, so you get 6 embryos to implant at a success rate of ~20% each which gives you about even odds for a healthy live birth, so you need to double the $5m.
CRISPR: $30? vs $5k for TALENs https://www.nature.com/articles/522020a “Zayner says the kits will contain everything a budding scientist needs to carry out CRISPR experiments on yeast or bacteria. For US$130, you can have a crack at re-engineering bacteria so that it can survive on a food it normally wouldn’t be able to handle, or for $160, you can get your eukaryote on and edit the ADE2 gene of yeast to give it a red pigment.” https://www.indiegogo.com/projects/diy-crispr-kits-learn-modern-science-by-doing https://www.thermofisher.com/us/en/home/life-science/genome-editing/geneart-crispr/crispr-cas9-based-genome-editing.html http://www.sigmaaldrich.com/technical-documents/articles/biology/crispr-cas9-genome-editing.html http://www.genscript.com/CRISPR-genome-edited-mammalian-cell-lines.html http://ipscore.hsci.harvard.edu/genome-editing-services http://www.blueheronbio.com/Services/CRISPR-Cas9.aspx http://www.addgene.org/crispr/ ‘Jennifer Doudna, one of the co-discoverers of CRISPR, told MIT Tech Review’s Antonio Regalado just how easy it was to work with the tool: “Any scientist with molecular biology skills and knowledge of how to work with [embryos] is going to be able to do this.” Harvard geneticist George Church, whose lab is doing some of the premier research on CRISPR, says: “You could conceivably set up a CRISPR lab for $2,000.”’ https://www.businessinsider.com/how-to-genetically-modify-human-embryos-2015-4 “Democratizing genetic engineering: This one should keep you up at night. CRISPR is so accessible-you can order the components online for $60-that it is putting the power of genetic engineering into the hands of many more scientists. But the next wave of users could be at-home hobbyists. This year, developers of a do-it-yourself genetic engineering kit began offering it for $700, less than the price of some computers. The trend might lead to an explosion of innovation-or to dangerous, uncontrolled experiments by newbies. Watch out, world.” https://www.technologyreview.com/s/543941/everything-you-need-to-know-about-crispr-gene-editings-monster-year/ “Individual plasmids can be ordered at $65 per plasmid, and will be shipped as bacterial stabs” https://www.addgene.org/crispr/yamamoto/multiplex-crispr-kit/ “At least since 195373ya, when James Watson and Francis Crick characterized the helical structure of DNA, the central project of biology has been the effort to understand how the shifting arrangement of four compounds-adenine, guanine, cytosine, and thymine-determines the ways in which humans differ from each other and from everything else alive. CRISPR is not the first system to help scientists pursue that goal, but it is the first that anyone with basic skills and a few hundred dollars’ worth of equipment can use.”CRISPR is the Model T of genetics,” Hank Greely told me when I visited him recently, at Stanford Law School, where he is a professor and the director of the Center for Law and the Biosciences. “The Model T wasn’t the first car, but it changed the way we drive, work, and live. CRISPR has made a difficult process cheap and reliable. It’s incredibly precise. But an important part of the history of molecular biology is the history of editing genes.”…“In the past, this would have taken the field a decade, and would have required a consortium,” Platt said. “With CRISPR, it took me four months to do it by myself.” In September, Zhang published a report, in the journal Cell, describing yet another CRISPR protein, called Cpf1, that is smaller and easier to program than Cas9.” https://www.newyorker.com/magazine/201511ya/11/16/the-gene-hackers?mbid=rss
2017 7% https://predictionbook.com/predictions/177110 2018 30% https://predictionbook.com/predictions/177114 2019 55% https://predictionbook.com/predictions/177115 by 2020, 75% https://predictionbook.com/predictions/177111
Whither embryo editing? The problem with IVF is that it is expensive, painful, and requires patience & planning. Even with large gains from editing, can we expect more than the current 1% or so of parents to ever be willing to conceive via IVF for those gains? If not, then the benefits may take generations to mix into the general population as offspring reproduce normally with unedited people and people happen to need to use IVF for regular fertility reasons. A solution is suggested by the adult CRISPR trials: make the germline edits in advance. In females, it seems like it might be hard to reach all the eggs which could potentially result in conception, but in males, sperm turnover is constant https://en.wikipedia.org/wiki/Spermatogenesis and sperm are replenished by stem cells in https://en.wikipedia.org/wiki/Seminiferous_tubule already demonstrated CRISPR edits to spermatogonia and subsequent inheritance by offspring: “Targeted Germline Modifications in Rats Using CRISPR/Cas9 and Spermatogonial Stem Cells”, et al 2014 https://www.sciencedirect.com/science/article/pii/S2211124715001989 “Genome Editing in Mouse Spermatogonial Stem Cell Lines Using TALENS and Double-Nicking CRISPR/Cas9”, et al 2015 https://www.sciencedirect.com/science/article/pii/S221367111500154X extraction, modification, and re-transplanting is likely also a no-fly, but the edits demonstrate that CRISPR will not interfere with reproduction, and so better delivery methods can be developed editing via two intravenous injections of a virus (carrying the editing template) and lipid-encapsulated Cas9-enzyme into the mice’ tail vein: et al 2016, yielding 6% of cells edited in the liver
https://en.wikipedia.org/wiki/Status_quo_bias “The Reversal Test: Eliminating Status Quo Bias in Applied Ethics”, 2006 https://ethicslab.georgetown.edu/phil553/wordpress/wp-content/uploads/201511ya/01/Ord-and-Bostrom-Eliminating-Status-Quo-Bias-in-Applied-Ethics-.pdf A mutation load review leads me to some hard figures from et al 2014 (supplement) using data from et al 2012; particularly relevant is figure 3, the number of single-nucleotide variants per person over the European-American sample, split by estimates of harm from least to most likely: 21345 + 15231 + 5338 + 1682 + 1969 = 45565. The supplementary tables gives a count of all observed SNVs by category, which sum to 300209 + 8355 + 220391 + 7001 + 351265 + 10293 = 897514, so the average frequency must be 45565/897514=0.05, and then the binomial SD will be sqrt(897514*0.05*(1-0.05))=206.47. https://en.wikipedia.org/wiki/Paternal_age_effect https://www.biorxiv.org/content/biorxiv/early/2016/03/08/042788.full.pdf “Older fathers’ children have lower evolutionary fitness across four centuries and in four populations” “Rate of de novo mutations and the importance of father’s age to disease risk” https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3548427/ “Novel variation and de novo mutation rates in population-wide de novo assembled Danish trios” https://www.nature.com/ncomms/201511ya/150119/ncomms6969/full/ncomms6969.html https://academic.oup.com/genetics/article/202/3/869/5930150 “Thus, keeping in mind that some mutations in repetitive DNA likely go undetected owing to mapping difficulties in genome-sequencing projects, with a diploid genome size of ~6 billion bases, an average newborn contains ~100 de novo mutations….Numerous studies with model organisms indicate that such effects have a broad distribution ( et al 1999; Halligan and 2009)-most mutations have minor effects, very few have lethal consequences, and even fewer are beneficial. In all organisms, the majority of mutations with effects on fitness reduce viability/fecundity by something on the order of 1% per mutation (; et al 2005; Eyre-Walker and 2007), and this class is thought to constitute 1-10% of all human mutations, the remainder being essentially neutral (Lindblad- et al 2011; 2012; et al 2014). Taking the lower end of the latter range suggests that the recurrent load of mutations imposed on the human population drags fitness down by 1% per generation, more so if the fraction of deleterious mutations exceeds 0.01 or if the environment is mutagenic, and less so if the average fitness effect of a mutation were to be <1%”
“Parental influence on human germline de novo mutations in 1,548 trios from Iceland”, et al 2017:
To understand how the age and sex of transmitting parents affect de novo mutations, here we sequence 1,548 Icelanders, their parents, and, for a subset of 225, at least one child, to 35× genome-wide coverage. We find 108,778 de novo mutations, both single-nucleotide polymorphisms and indels, and determine the parent of origin of 42,961. The number of de novo mutations from mothers increases by 0.37 per year of age (95% CI 0.32-0.43), a quarter of the 1.51 per year from fathers (95% CI 1.45-1.57). The number of clustered mutations increases faster with the mother’s age than with the father’s, and the genomic span of maternal de novo mutation clusters is greater than that of paternal ones.
…To assess differences in the rate and class of DNMs transmitted by mothers and fathers, we analysed whole-genome sequencing (WGS) data from 14,688 Icelanders with an average of 35x coverage (Data Descriptor^19). This set contained 1,548 trios, used to identify 108,778 high-quality DNMs (101,377 single-nucleotide polymorphisms (SNPs); Methods and Fig. 1), resulting in an average of 70.3 DNMs per proband. The DNM call quality was also assessed using 91 monozygotic twins of probands (Method). Of 6,034 DNMs observed in these probands, 97.1% were found in their twins. Sanger sequencing was used to validate 38 discordant calls in monozygotic twins, of which 57.9% were confirmed to be present only in the proband, and therefore postzygotic, with the rest deemed genotyping errors.
…Mutation rates are key parameters for calibrating the timescale of sequence divergence. We estimate the mutation rate as 1.29 × 10-8 per base pair per generation and 4.27 × 10-10 per base pair per year (Method). Our findings have a direct bearing on the disparity that has emerged between mutation rates estimated directly from pedigrees (~4 × 10-10 per base pair per year) and phylogenetic rates (~10-9 per base pair per year)3, as they indicate that the molecular clock is affected by life-history traits in a sex-specific manner23-25 and varies by genomic region within and across species. This allows us to predict the long-term consequences of a shift in generation times (Method)24. Thus, a 10 year increase in the average age of fathers would increase the mutation rate by 4.7% per year. The same change for mothers would decrease the mutation rate by 9.6%, because extra mutations attributable to older mothers are offset by fewer generations
“Genome Graphs and the Evolution of Genome Inference”, et al 2017:
From short-read based assays, it is estimated that the average diploid human has between 4.1 and 5 million point mutations, either single-nucleotide variants (SNVs), multi-nucleotide variants (MNVs), or short indels, which is only around 1 point variant every 1450 to 1200 bases of haploid sequence ( et al 2015). Such an average human would also have about 20 million bases-about 0.3% of the genome-affected by around 2,100-2,500 larger structural variants (). It should be noted that both these estimates are likely somewhat conservative as some regions of the genome are not accurately surveyed by the short read technology used. Indeed, long read sequencing demonstrates an excess of structural variation not found by earlier short read technology ( et al 2015; et al 2016).
http://gnxp.com/2017/04/15/genetic-variation-in-human-populations-and-individuals/
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3155974/ “Genetic costs of domestication and improvement” et al 2017 https://www.biorxiv.org/content/early/2017/03/29/122093.full
“The demographic history and mutational load of African hunter-gatherers and farmers”, et al 2017 https://www.biorxiv.org/content/early/2017/04/26/131219.full
“(This dataset includes 463 million variants on 62784 individuals. Click here to switch to Freeze3a on GRCh37/hg19.)” https://bravo.sph.umich.edu/freeze5/hg38/
“Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection”, et al 2017:
Recent work has hinted at the linkage disequilibrium (LD)-dependent architecture of human complex traits, where SNPs with low levels of LD (LLD) have larger per-SNP heritability. Here we analyzed summary statistics from 56 complex traits (average N = 101,401) by extending stratified LD score regression to continuous annotations. We determined that SNPs with low LLD have significantly larger per-SNP heritability and that roughly half of this effect can be explained by functional annotations negatively correlated with LLD, such as DNase I hypersensitivity sites (DHSs). The remaining signal is largely driven by our finding that more recent common variants tend to have lower LLD and to explain more heritability (P = 2.38 × 10−104); the youngest 20% of common SNPs explain 3.9 times more heritability than the oldest 20%, consistent with the action of negative selection. We also inferred jointly significant effects of other LD-related annotations and confirmed via forward simulations that they jointly predict deleterious effects.
Understanding the role of rare variants is important in elucidating the genetic basis of human diseases and complex traits. It is widely believed that negative selection can cause rare variants to have larger per-allele effect sizes than common variants. Here, we develop a method to estimate the minor allele frequency (MAF) dependence of SNP effect sizes. We use a model in which per-allele effect sizes have variance proportional to [p(1-p)]α, where p is the MAF and negative values of α imply larger effect sizes for rare variants. We estimate α by maximizing its profile likelihood in a linear mixed model framework using imputed genotypes, including rare variants (MAF >0.07%). We applied this method to 25 UK Biobank diseases and complex traits (N=113,851). All traits produced negative α estimates with 20 significantly negative, implying larger rare variant effect sizes. The inferred best-fit distribution of true α values across traits had mean -0.38 (s.e. 0.02) and standard deviation 0.08 (s.e. 0.03), with statistically-significant heterogeneity across traits (P=0.0014). Despite larger rare variant effect sizes, we show that for most traits analyzed, rare variants (MAF <1%) explain less than 10% of total SNP-heritability. Using evolutionary modeling and forward simulations, we validated the α model of MAF-dependent trait effects and estimated the level of coupling between fitness effects and trait effects. Based on this analysis an average genome-wide negative selection coefficient on the order of 10-4 or stronger is necessary to explain the α values that we inferred.
SNPs have two relevant properties: a frequency of being zero, and an effect size
Benyamin polygenic score distribution: looks either exponential or log-normal and a Cullen & Frey graph indicates it is closes to exponential & log-normal distributions.
library(fitdistrplus)
with(benyamin[benyamin$EFFECT_A1>0,], descdist(abs(EFFECT_A1)/15, discrete=FALSE))
fit.exp <- with(benyamin[benyamin$EFFECT_A1>0,], fitdist(abs(EFFECT_A1)/15, "exp")); fit.exp
# Fitting of the distribution ' exp ' by maximum likelihood
# Parameters:
# estimate Std. Error
# rate 1063.15695 1.281452665
fit.ln <- with(benyamin[benyamin$EFFECT_A1>0,], fitdist(abs(EFFECT_A1)/15, "lnorm")); fit.ln
# Fitting of the distribution ' lnorm ' by maximum likelihood
# Parameters:
# estimate Std. Error
# meanlog -7.402017853 0.0013198365617
# sdlog 1.095050030 0.0009332618808Plotting residuals & diagnostics, the log-normal performs much worse due to overestimating the number of near-zero effects (the Q-Q plot is particularly bad), so we’ll use the exponential for effect sizes
As proportions, the frequencies are probably close to either uniform or beta distributions; in this case, they are very nearly uniformly distributed 0-1:
fitdist(benyamin$FREQ_A1, "beta", method="mme")
# Fitting of the distribution ' beta ' by matching moments
# Parameters:
# estimate
# shape1 1.065412339
# shape2 1.126576711Set up: 50k SNPs, true effect sizes are exponentially distributed with exponential(rate=1063.15695), frequencies distributed beta(1.065412339, 1.126576711) can’t do full simulation of 500k SNPs with 100k datapoints, not enough RAM given inefficient R format for booleans: (100000 * 100000 * 48 bytes) / 1000000000 ; 4.8e+11 bytes or 480GB can JAGS even handle that much data?
SNPs <- 500000
SNPlimit <- 50000
N <- 10000
genes <- data.frame(Effects = sort(rexp(SNPs, rate=1063.15695), decreasing=TRUE)[1:SNPlimit], Frequencies = rbeta(SNPlimit, shape1=1.065412339, shape2=1.126576711))
person <- function() { rbinom(SNPlimit, 1, prob=genes$Frequencies) }
test <- as.data.frame(t(replicate(N, person())))
format(object.size(test), units="GB")
# [1] "1.9 Gb"
test$Polygenic.score <- sapply(1:nrow(test), function(i) { sum(ifelse(test[i,], genes$Effects, 0)) })
test$IQ <- 100 + 15 * rnorm(N, mean=scale(test$Polygenic.score), sd=sqrt(1-0.33))
library(BGLR)
b <- BGLR(test$IQ, ETA=list(list(X=test[,1:SNPlimit], model="BL", lambda=202, shape=1.1, rate=2.8e-06)), R2=0.33)
gc()BGLR problem: I can’t scale it to n=100k/SNP=500k, BGLR RAM consumption maxes out at n=10k/SNP=50k. This wouldn’t be a problem for the Thompson sampling, but I need to use JAGS anyway for that. So BGLR can’t give me posteriors for et al 2013 or 2014 data.
can do Bayesian GWAS from public summary statistics using RSS “Bayesian large-scale multiple regression with summary statistics from genome-wide association studies” https://www.biorxiv.org/content/biorxiv/early/2016/03/04/042457.full.pdf Matlab library https://github.com/stephenslab/rss installation: https://github.com/stephenslab/rss/wiki/RSS-via-MCMC RSS example 1 https://github.com/stephenslab/rss/wiki/Example-1 code: https://github.com/stephenslab/rss/blob/master/examples/example1.m data https://uchicago.app.box.com/example1 doesn’t run under Octave at the moment although I got it close: https://github.com/stephenslab/rss/issues/1 what are my alternatives? RSS is the best looking Bayesian one so far. I can try pirating Matlab, or apparently the Machine Learning Coursera gives one a temporary 120-day subscription
groundTruth <- function(alleles, causal, genotype) {
score <- rnorm(1, mean=100, sd=15)
for (i in 1:length(genotype)) {
if(causal[i] && genotype[i]) { print(alleles[i]); score <- score + alleles[i]; } }
return(score);}
alleles <- sort(rexp(10000, rate=70), decreasing=TRUE)[1:10]
causal <- c(TRUE, rep(FALSE, 8), TRUE)
df <- data.frame()
for(i in 1:50) {
genotype <- rbinom(n=10,1,prob=0.50)
IQ <- groundTruth(alleles, causal, genotype)
df <- rbind(df, c(IQ, genotype))
}
names(df) <- c("IQ", "A", "B", "C", "D", "E", "F", "G", "H", "I", "J")
library(reshape2)
df2 <- melt(df, "IQ")
model1 <- function() {
for (i in 1:N) {
for (j in 1:K) {
b[j] ~ dexp(70)
y[i] ~ dnorm(100, 0.06) + b[j]
}
}
}
data1 <- list(N=nrow(df2), K=10, y=df2$IQ, b=1:length(unique(df2$variable)))
jags(data=data1, parameters.to.save="b", model.file=model1)
# eg. groundTruth(c(TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, FALSE, FALSE))
simulate <- function(a, c) {
}
library(runjags)
model1 <- "model {
for (i in 1:N) {
y[i] ~ dnorm(mu[i], tau[i])
mu[i] <- muOfClust[ clust[i] ]
clust[i] ~ dcat(pi[])
}
for (i in 1:K) {
pi[i] <- 0.05
muOfClust[i] ~ dexp(70)
tau[i] ~ dgamma(1.0E-3, 1.0E-3)
}
}"
j1 <- autorun.jags(model1, monitor=c("theta"), data = list(N=nrow(oldData2), y=oldData2$Yes, n=oldData2$N, switch=c(0.5, 0.5), clust=c(1,NA))); j1
# ... Lower95 Median Upper95 Mean SD Mode MCerr MC%ofSD SSeff AC.10 psrf
# theta[1] 0.70582 0.75651 0.97263 0.77926 0.07178 -- 0.001442 2 2478 0.12978 1.0011
# theta[2] 0.72446 0.75078 0.77814 0.75054 0.013646 -- 0.00009649 0.7 20000 0.009458 1https://github.com/jeromyanglim/JAGS_by_Example/blob/master/03-multilevel/varying-intercept-long/varying-intercept-long.rmd http://doingbayesiandataanalysis.blogspot.com/201214ya/06/mixture-of-normal-distributions.html https://www.stats.ox.ac.uk/~bardenet/Material/mixture_with_jags_only_mu.html
“Genome-wide association study identifies 74 [162] loci associated with educational attainment”, et al 2016 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4883595/ supplementary info: https://media.nature.com/original/nature-assets/nature/journal/v533/n7604/extref/nature17671-s1.pdf https://media.nature.com/original/nature-assets/nature/journal/v533/n7604/extref/nature17671-s2.xlsx https://www.thessgac.org/#!data/kuzq8 https://ssgac.org/documents/FAQ_74_loci_educational_attainment.pdf
Educational attainment is strongly influenced by social and other environmental factors, but genetic factors are estimated to account for at least 20% of the variation across individuals1. Here we report the results of a genome-wide association study (GWAS) for educational attainment that extends our earlier discovery sample1, 2 of 101,069 individuals to 293,723 individuals, and a replication study in an independent sample of 111,349 individuals from the UK Biobank. We identify 74 [162 total] genome-wide significant loci associated with the number of years of schooling completed. Single-nucleotide polymorphisms associated with educational attainment are disproportionately found in genomic regions regulating gene expression in the fetal brain. Candidate genes are preferentially expressed in neural tissue, especially during the prenatal period, and enriched for biological pathways involved in neural development. Our findings demonstrate that, even for a behavioral phenotype that is mostly environmentally determined, a well-powered GWAS identifies replicable associated genetic variants that suggest biologically relevant pathways. Because educational attainment is measured in large numbers of individuals, it will continue to be useful as a proxy phenotype in efforts to characterize the genetic influences of related phenotypes, including cognition and neuropsychiatric diseases.
Using procedures identical to those described in SI §1.6, we conducted a meta-analysis of the EduYears phenotype, combining the results from our discovery cohorts (n = 293,723) and the results from the UKB replication cohort (n = 111,349). Expanding the overall sample size to N = 405,072 increases the number of approximately independent genome-wide significant loci 74 → 162.
…This background suffices to motivate the biological questions that arise in the interpretation of GWAS results and the means by which these questions might be tentatively addressed. For starters, since a GWAS locus typically contains many other SNPs in LD with the defining lead SNP and with each other, it is natural to ask: which of these SNPs is the actual causal site responsible for the downstream phenotypic variation? Many SNPs in the genome appear to be biologically inert-neither encoding differences in protein composition nor affecting gene regulation-and a lead GWAS SNP may fall into this category and nonetheless show the strongest association signal as a result of statistical noise or happenstance LD with multiple causal sites. Fortunately, much is known from external sources of data about whether variation at a particular site is likely to have biological consequences, and exploiting these resources is our general strategy for fine-mapping loci: nominating individual sites that may be causally responsible for the GWAS signals. Descriptions of genomic sites or regions based on external sources of data are known as annotations, and readers will not go far astray if they interpret this term rather literally (as referring to a note of explanation or comment added to a text in one of the margins). If we regard the type genome as the basic text, then annotations are additional comments describing the structural or functional properties of particular sites or the regions in which they reside. For example, all nonsynonymous sites that influence protein structures might be annotated as such. An annotation can be far more specific than this; for instance, all sites that fall in a regulatory region active in the fetal liver might bear an annotation to this effect. A given causal site will exert its phenotypic effect through altering the composition of a gene product or regulating its expression. Conceptually, once a causal site has been identified or at least nominated, the next question to pursue is the identity of the mediating gene. In practice, because only a handful of genes at most will typically overlap a GWAS locus, we can make some progress toward answering this question without precise knowledge of the causal site. The difficulty of the problem, however, should still not be underestimated. It is natural to assume that a lead GWAS SNP lying inside the boundaries of a particular gene must reflect a causal mechanism involving that gene itself, but in certain cases such a conclusion would be premature. It is possible for a causal SNP lying inside a certain gene to exert its phenotypic effect by regulating the expression of a nearby gene or for several genes to intervene between the SNP and its regulatory target. Supplementary Table 4.1 ranks each gene overlapping a DEPICT-defined locus by the number of discrete evidentiary items favoring that gene (see Supplementary Information §4.5 for details regarding DEPICT). These lines of evidence are taken from a number of our analyses to be detailed in the following subsections. Our primary tool for gene prioritization is DEPICT, which can be used to calculate a P-value and associated FDR for each gene. It is important to keep in mind, however, that a gene-level P-value returned by DEPICT refers to the tail probability under the null hypothesis that random sampling of loci can account for annotations and patterns of co-expression shared by the focal gene with genes in all other GWAS-identified loci. Although it is very reasonable to expect that genes involved in the same phenotype do indeed share annotations and patterns of co-expression, it may be the case that certain causal genes do not conform to this expectation and thus fail to yield low DEPICT P-values. This is why we do not rely on DEPICT alone but also the other lines of evidence described in the caption of Supplementary Table 4.1.
However, a priori we know that some SNPs are more likely to be associated with the phenotype than others; for example, it is often assumed that nonsynonymous SNPs are more likely to influence phenotypes than sites that fall far from all known genes. So a P-value of 5×10 −7 , say, though not typically considered significant at the genome-wide level, might merit a second look if the SNP in question is nonsynonymous. Formalizing this intuition can be done with Bayesian statistics, which combines the strength of evidence in favor of a hypothesis (in our case, that a genomic site is associated with a phenotype) with the prior probability of the hypothesis. Deciding how to set this prior is often subjective. However, if many hypotheses are being tested (for example, if there are thousands of nonsynonymous polymorphisms in the genome), then the prior can be estimated from the data themselves using what is called “empirical Bayes” methodology. For example, if it turns out that SNPs with low P-values tend to be nonsynonymous sites rather than other types of sites, then the prior probability of true association is increased at all nonsynonymous sites. In this way a nonsynonymous site that otherwise falls short of the conventional significance threshold can become prioritized once the empirically estimated prior probability of association is taken into account. Note that such favorable reweighting of sites within a particular class is not set a priori, but is learned from the GWAS results themselves. In our case, we split the genome into approximately independent blocks and estimate the prior probability that each block contains a causal SNP that influences the phenotype and (within each block) the conditional prior probability that each individual SNP is the causal one. Each such probability is allowed to depend on annotations describing structural or functional properties of the genomic region or the SNPs within it. We can then empirically estimate to extent to each annotation predicts association with the focal phenotype. For a complete description of the fgwas method, see ref. 1. 4.2.3 Methods For application to the GWAS of EduYears, we used the same set of 450 annotations as ref. 1; these are available at https://github.com/joepickrell/1000-genomes. …4.2.6 Reweighted GWAS and Fine Mapping We reweighted the GWAS results using the functional-genomic results described above. Using a regional posterior probability of association (PPA) greater than 0.90 as the cutoff, we identified 102 regions likely to harbor a causal SNP with respect to EduYears (Extended Data Fig. 7c and Supplementary Table 4.2.1). All but two of our 74 lead EduYears-associated SNPs fall within one of these 102 regions. The exceptions are rs3101246 and rs2837992, which attained PPA > 0.80 (Extended Data Fig. 7c). In previous applications of fgwas, the majority of novel loci that attained the equivalent of genome-wide significance only upon reweighting later attained the conventional P < 5×10 −8 in larger cohorts 1 . Within each region attaining PPA > 0.90, each SNP received a conditional posterior probability of being the causal SNP (under the assumption that there is just one causal SNP in the region). The method of assigning this latter posterior probability is similar to that of ref. 6, except that the input Bayes factors are reweighted by annotation-dependent and hence SNP-varying prior probabilities. In essence, the likelihood of causality at an individual SNP derives from its Bayes factor with respect to phenotypic association (which is monotonically related to the P-value under reasonable assumptions), whereas the prior probability is derived from any empirical genome-wide tendency for the annotations borne by the SNP to predict evidence of association. Thus, the SNP with the largest posterior probabilities of causality tend to exhibit among the strongest P-values within their loci and functional annotations that predict association throughout the genome. Note that proper calibration of this posterior probability requires that all potential causal sites have been either genotyped or imputed, which may not be the case in our application; we did not include difficult-to-impute non-SNP sites such as insertions/deletions in the GWAS meta-analysis. With this caveat in mind, we identified 17 regions where fine mapping amassed over 50 percent of the posterior probability on a single SNP (Supplementary Table 4.2.2). Of our 74 lead EduYears SNPs, 9 are good candidates for being the causal sites driving their association signals [12%]. One of our top SNPs, rs4500960, is in nearly perfect LD with the causal candidate rs2268894 (and is indeed the second most likely causal SNP in this region according to fgwas). The causal candidate rs6882046 is within 75kb of two lead SNPs on chromosome 5 (rs324886 and rs10061788), but no two of these three SNPs show strong LD. Interestingly, the remaining 6 causal candidates lie in genomic regions that only attain the equivalent of genome-wide significance upon Bayesian reweighting. Of the 17 causal candidates, 9 lie in regions that are DNase I hypersensitive in the fetal brain.
Table 4.2.2:
Posterior Probability of Causality
0.992035 0.766500 0.842271 0.567184 0.697862 0.524760 0.632536 0.885280 0.968627 0.781563 0.629610 0.837746 0.725158 0.755457 0.784373 0.682947 0.832675
[
mean(c(0.524760, 0.567184, 0.629610, 0.632536, 0.682947, 0.697862, 0.725158, 0.755457, 0.766500, 0.781563, 0.784373, 0.832675, 0.837746, 0.842271, 0.885280, 0.968627, 0.992035))= 0.76, 0.76*19=14.4]The results from both approaches show that prediction accuracy increases as more SNPs are used to construct the score, with the maximum predictive power achieved when using all the genotyped SNPs (with Approach 1). In that case, the weighted average across the two cohorts of the incremental R 2 is ~3.85%.
[Versus 2% from Rietveld’s n=100k; this is in line with the rough doubling of the main SSGAC sample size. The additional UK Biobank sample of n=111k does not seem to have been used but if it was used, should boost the polygenic score to ~5.3%?]
…The magnitude of predictive power that we observe is less than one might have expected on the basis of statistical genetics calculations 6 and GCTA-GREML estimates of “SNP heritability” from individual cohorts. Indeed, et al 2013 7 reported GCTA-GREML estimates of SNP heritability for each of two cohorts (STR and QIMR), and the mean estimate was 22.4%. Assuming that 22.4% is in fact the true SNP heritability, the calculations outlined in the SOM of Rietveld et al (pp. 22-23) generate a prediction of R 2 = 11.0% for a score constructed from the GWAS estimates of this paper and of R 2 = 6.1% for a score constructed from the combined (discovery + replication cohorts, but excluding the validation cohorts) GWAS sample of N ≈ 117,000-119,000 in Rietveld et al.-substantially higher than the 3.85% that we achieve here (with the score based on all genotyped SNPs) and the 2.2% Rietveld et al. achieved, respectively.
These discrepancies between the scores’ predicted and estimated R 2 may be due to the failure of some of the assumptions underlying the calculation of the predicted R 2 . An alternative (or additional) explanation is that the true SNP heritability for the GWAS sample pooled across cohorts is lower than 22.4%. That would be the case if the true GWAS coefficients differ across cohorts, perhaps due to heterogeneity in phenotype measurement or gene-by-environment interactions. If so, then a polygenic score constructed from the pooled GWAS sample would be expected to have lower predictive power in an individual cohort than implied by the calculations above. Based on that reasoning, the R 2 of 2.2% observed by et al 2013 could be rationalized by assuming that the proportion of variance accounted for by common variants across the pooled Rietveld cohorts is only 12.7% 6 . (We obtain a similar estimate, 11.5% with a standard error of 0.45%, when we use LD Score regression 5 to estimate the SNP heritability using our pooled-sample meta-analysis results from this paper, excluding deCODE and without GC. While we believe this estimate is based on cohort results without GC, it is biased downward if any cohort in fact applied GC.) If we assume that the 12.7% is valid also for the cohorts considered in this study, we would predict an R 2 equal to 4.5%, somewhat higher than we observe in HRS and STR but much closer. However, the degree of correlation in coefficients across cohorts appears to be relatively high (Supplementary Table 1.10 reports estimates of the genetic correlation between selected cohorts and deCODE; although the correlation estimates vary a lot across cohorts, they tend to be large for the largest cohorts, and the weighted average is 0.76). We do not know whether a pooled-cohort SNP heritability of 12.7% or lower can be reconciled with the observed degree of correlation in coefficients across cohorts.
The results are reported in Supplementary Tables 6.3 and 6.4. In both the STR and the HRS, cognitive performance significantly mediates the effect of PGS on EduYears; in the HRS, Openness to Experience is also a significant mediator. The indirect effects for the other mediating variables are not significant s . The results for cognitive performance are similar across STR and HRS. In both datasets, a one-standard deviation increase in PGS is associated with ~0.6-0.7 more years of education, and a one-standard deviation increase in cognitive performance is associated with ~0.15 more years of education. In both datasets, the direct effect (θ 1 ) of PGS on EduYears is ~0.3-0.4 and the total indirect effect (β 1 θ 2 ) is ~0.19-0.31. This implies that a one-standard-deviation increase in PGS is associated with ~0.3-0.4 more years of education, keeping the mediating variables constant, and that changing the mediating variables to the levels they would have attained had PGS increased by one standard deviation (but keeping PGS fixed) increases years of education by ~0.19-0.31 years. Lastly, in both datasets, the partial indirect effect (θ 21 β 11 ) of cognitive performance is large and very significant: the estimates are equal to 0.29 and 0.14-or 42% and 23% of the total effect (γ 1 )-in STR and HRS, respectively. The results also suggest that a one-standard deviation increase in Openness to Experience is associated with ~0.06 more years of education, and the estimated partial indirect effect for Openness to Experience is equal to 0.04-or 7% of the total effect (γ 1 ).
Fine-mapping: “Association mapping of inflammatory bowel disease loci to single variant resolution”, et al 2017 https://www.biorxiv.org/content/early/201511ya/10/20/028688.full et al 2015 et al 2013 van de et al 2015 “Evaluating the Performance of Fine-Mapping Strategies at Common Variant GWAS Loci” 1https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1005535 “Refining the accuracy of validated target identification through coding variant fine-mapping in type 2 diabetes”, et al 2018: fine-mapping suggests maybe a quarter of hits are causal?
let’s say we have 74 SNP candidates with 2 levels each (on/off) which collectively determine the dependent variable IQ with an effect of +0.2 IQ points or +0.0133SDs each; we want power=0.80/alpha=0.05 to detect the main effect for each SNP to see if it has a non-zero effect. In factorial ANOVA terms, this would be a design with 74^2=5476 possible conditions (since we are only interested in main effects and not interactions, I think it could be a partial factorial design where many of those are dropped). As a multiple regression, it’d be something like IQ ~ A + B + C + ... ZZ. The effect of each variable is quite small, and so adding them all into a linear model will explain only a small amount of variance: (0.2/15)^2 * 74 = 0.0132.
G*Power 3.1 (http://www.gpower.hhu.de/ Windows version under Wine), test family ‘F test’, statistical test ‘Linear multiple regression: Fixed model, R increase’, a priori power analysis:
l = 0.0133766? n=2711
Suppose we have a budget of 64 edits per embryo, and we want to be able to fill them all up with causal variants; we know that around half will already be the good variant, so we need to have at least 642=128 causal variants. And since we know that each SNP candidate has a ~10% probability of being causal, we need to be testing 10 128 = >1280 SNPs to successfully winnow down to >128 causal SNPs which will yield >64 available edits.
We’ll drop the mean effect to 0.1 points and consider sample size requirements testing 1280 SNPs. (0.1/15)^2 * 1280 = 0.05688888889
l=0.06032045 n=2954
What does 80% power and 5% alpha mean here? We know that ~10% are causal (our base rate for a true finding is 10%), so there are 128 causal SNPs and 1152 noncausal SNPs here. There is a 5% false positive rate, so there will be 0.051152=58 false positive SNPs. There is 80% power, so we will detect 0.8128=102 causal SNPs. So we will have 58+102=160 apparently causal SNPs, but only 58/160=36% are actually causal. So we waste 64% of our edits. We need to do better.
let’s try with 0.9 and 0.01
l=0.06032045 n=3987
0.90.11280=115 0.01*(1280-115)=11 115/(115+11)=0.91
0.1 average effect might be optimistic even though effect sizes decline slowly, so one last try with 0.05 mean effect size over those 1280 SNPs: (0.05/15)^2 * 1280 = 0.0142
l = 0.0144045 n=14197
n <- 1000
alpha <- 0.005
SNP_candidates <- 162
SNP_mean_effect <- 0.2
SNP_mean_frequency <- 0.5
SNP_causal_probability <- 0.12
SNP_effects <- sample(c(SNP_mean_effect, 0), SNP_candidates, replace=TRUE,
prob=c(SNP_causal_probability, 1-SNP_causal_probability))
which(SNP_effects>0)
r2 <- 0.01
generateSample <- function(n, SNP_effects, SNP_candidates=162, SNP_mean_frequency=0.5) {
dm <- matrix(nrow=n, ncol=SNP_candidates+1)
for (i in 1:n) {
SNP_draw <- rbinom(SNP_candidates, 1, p=SNP_mean_frequency)
SNPs_genetic <- sum(ifelse(SNP_draw, SNP_effects, 0))
IQ <- rnorm(1, mean=100, sd=15) + SNPs_genetic
dm[i,] <- c(round(IQ), SNP_draw)
}
df <- as.data.frame(dm)
colnames(df) <- c("IQ", paste("SNP.", as.character(1:SNP_candidates), sep=""))
return(df)
}
df <- generateSample(n, SNP_effects, SNP_candidates, SNP_mean_frequency)
power <- sapply(seq(1, n, by=500), function(i) {
l <- summary(lm(IQ ~ ., data=df[1:i,]))
# coefficients <- l$coefficients[,1]
pvalues <- l$coefficients[,4][-1]
causalPvalues <- na.omit(ifelse(SNP_effects>0, pvalues, NA))
noncausalPvalues <- na.omit(ifelse(SNP_effects==0, pvalues, NA))
alphas <- seq(from=0.001, to=0.05, by=0.001)
alphaYields <- sapply(alphas, function(alpha) { sum(causalPvalues<alpha) / (sum(pvalues<alpha)) })
alpha <- alphas[which.max(alphaYields)]
positives <- sum(pvalues<alpha)
falsePositives <- sum(noncausalPvalues<alpha)
truePositives <- sum(causalPvalues<alpha)
truePositiveFraction <- truePositives / length(causalPvalues)
causalFraction <- (truePositives + falsePositives) / positives
return(causalFraction) })
library(BGLR)
# n <- 1000
ns <- seq(100, 50000, by=400)
recovery <- sapply(ns, function(n) {
mean(replicate(100, {
## bootstrap a new dataset
d <- df[sample(nrow(df), n, replace=TRUE),]
b <- BGLR(d$IQ, ETA=list(list(X=d[-1], model="BayesB", probIn=SNP_causal_probability)), R2=0.01, burnIn=0, verbose=FALSE)
# plot((b$ETA[[1]]$b), SNP_effects!=0)
estimate <- data.frame(Causal=SNP_effects!=0, Estimate=(b$ETA[[1]]$b))
estimate <- estimate[order(estimate$Estimate),]
truePositives <- sum(estimate$Causal[1:64])
falseNegatives <- sum(estimate$Causal[-(1:64)])
# truePositives;falseNegatives
causalFraction <- truePositives / (truePositives+falseNegatives)
print(causalFraction)
return(causalFraction)
})) })
recovery
library(ggplot2)
qplot(ns, recovery) + geom_smooth(method=lm)
library(glmnet)
cv <- cv.glmnet(as.matrix(df[-1]), df$IQ)
g <- glmnet(as.matrix(df[-1]), df$IQ, lambda=cv$lambda.min)
coef(g)
causalSNPs <- which(SNP_effects>0)
ridgeSNPs <- which(as.matrix(coef(g)[-1,])!=0)
intersect(causalSNPs, ridgeSNPs)
length(intersect(causalSNPs, ridgeSNPs)) / length(causalSNPs)
length(intersect(causalSNPs, ridgeSNPs)) / length(ridgeSNPs)
Thompson sampling with a subset/edit budget:
SNP_edit_limit <- 100
SNP_candidates <- 500
verbose <- TRUE
SNP_mean_effect <- 0.2
SNP_mean_frequency <- 0.5
SNP_causal_probability <- 0.12
r2 <- 0.05
iqError <- 0.55 ## 5yo IQ scores correlate r=0.55 with adult
SNP_effects <- sample(c(SNP_mean_effect, 0), SNP_candidates, replace=TRUE,
prob=c(SNP_causal_probability, 1-SNP_causal_probability))
which(SNP_effects>0)
measurementError <- function(r, IQ) {
IQ.true.std <- (IQ-100)/15
IQ.measured.std <- r*IQ.true.std + rnorm(length(IQ), mean=0, sd=sqrt(1 - r^2))
IQ.measured <- 100 + 15 * IQ.measured.std
return(IQ.measured) }
generateExperimentalSample <- function(n, r, SNP_effects, SNP_candidates, SNP_mean_frequency, SNP_draw_generator) {
dm <- matrix(nrow=n, ncol=SNP_candidates+1+1) ## allocate space for all SNPs, true IQ, and measured IQ
for (i in 1:n) {
SNP_draw <- SNP_draw_generator() # which SNPs to toggle
SNPs <- ifelse(SNP_draw, SNP_effects, 0) ## convert to effects
SNP_genetic_score <- sum(SNPs, na.rm=TRUE)
## generate a N(100,15) - minus however much our candidate genes explain
IQ <- round(rnorm(1, mean=100, sd= sqrt((15^2) * (1-r2))) + SNP_genetic_score)
IQ_measured <- round(measurementError(r, IQ))
dm[i,] <- c(IQ, IQ_measured, SNP_draw)
}
df <- as.data.frame(dm)
colnames(df) <- c("IQ", "IQ.measured", paste("SNP.", as.character(1:SNP_candidates), sep=""))
return(df)
}
generateRandomSample <- function(n, r=1, SNP_effects, SNP_candidates, SNP_mean_frequency) {
generateExperimentalSample(n, r, SNP_effects, SNP_candidates, SNP_mean_frequency,
function() { rbinom(SNP_candidates, 1, p=SNP_mean_frequency) })
}
d <- generateRandomSample(1000, iqError, SNP_effects, SNP_candidates, SNP_mean_frequency)
summary(d)
library(BGLR)
library(ggplot2)
maximumDays <- 10000
batch <- 10
lag <- 5*365
jumpForward <- lag*5
## initialize with a seed of n>=2; with less or an empty dataframe, BGLR will crash
d <- generateRandomSample(jumpForward, iqError, SNP_effects, SNP_candidates, SNP_mean_frequency)
d$Date <- 1:jumpForward
# d$Date <- -lag # available immediately
regretLog <- data.frame(N=integer(), N.eff=integer(), Regret=numeric(), Fraction.random=numeric(), Fraction.causals=numeric(), Causal.found=integer(), Causal.notfound=integer())
for (i in jumpForward:maximumDays) {
## i=date; day 1, day 2, etc. A datapoint is only available if it was created more than 'lag' days ago; ie if we do 1 a day, then on day 20 with lag 18
## we will have 20-18=2 datapoints available. With a 5 year lag, we will go 1825 time-steps before any new data starts becoming available.
dAvailable <- d[i >= (d$Date+lag),]
## quick Bayesian model of our data up to now, using Lasso priors and our SNP setup
## BGLR will randomly crash with a gamma/lambda range error every ~5k calls, so catch & retry until it succeeds:
while(TRUE) {
tryCatch({
b <- BGLR(dAvailable$IQ.measured, ETA=list(list(X=dAvailable[-c(1, 2, length(colnames(dAvailable)))],
model="BL", type="beta", probIn=0.12, counts=162, R2=r2, lambda=202, max=500)),
verbose=FALSE)
means <- b$ETA[[1]]$b; sds <- b$ETA[[1]]$SD.b
break;
}, error = function(e) { print(e) })
}
## Thompson sampling: for Thompson sampling, we sample 1 possible value of each parameter from that parameter's
## posterior distribution. Normally, we would sample from the posterior samples returned by JAGS, but BGLR returns
## instead a mean+SD, so we sample from each parameter's normal distribution defined by the mean/sd. Then we see if it
## was positive (and hence worth editing); if it is positive, then we choose to edit it and toggle it to '1' (since
## we set the problem up as 1=increasing). This boolean is then passed into the simulation and a fresh datapoint generated according to
## that intervention. In the next loop, this new datapoint will be incorporated into the posterior and so on.
## For multiple-edit Thompson sampling where we can only edit _l_ out of _k_ possible SNPs, we sample 1 possible value
## as before, then we sort and take the top _l_ out of _k_ actions;
## then to decide whether to sample 1 or 0 in each arm, we do a second Thompson sample within each arm.
##
## To save computations while simulating, or to be more realistic, we might have batches: multiple datapoints in between
## updates. If batch=1, it is the conventional Thompson sample (and most data-efficient) but computationally demanding
## In the delayed-updates setting, 'batch' is how many get created each day
for (j in 1:batch) {
SNPs_Thompson_sampled <- function () {
## select the _l_ arms
samplesArms <- rnorm(n=SNP_candidates, mean=means, sd=sds)
cutoff <- sort(samplesArms, decreasing=TRUE)[SNP_edit_limit]
l <- which(samplesArms>=cutoff)
## for each winner, do another Thompson sample, and record the losers as NA/not-played
choices <- rep(NA, SNP_candidates)
samplesActions <- rnorm(n=SNP_edit_limit, mean=means[l], sd=sds[l]) > 0
choices[l] <- samplesActions
return(choices)
}
newD <- generateExperimentalSample(1, iqError, SNP_effects, SNP_candidates, SNP_mean_frequency, SNPs_Thompson_sampled)
newD$Date <- i
d <- rbind(d, newD)
}
## reports, evaluations, logging:
estimate <- data.frame(Causal=SNP_effects!=0, Effect=SNP_effects, Estimate=(b$ETA[[1]]$b), SD=b$ETA[[1]]$SD.b)
estimate <- estimate[order(estimate$Estimate, decreasing=TRUE),]
regretLog[i,]$Causal.found <- sum(estimate$Causal[1:SNP_edit_limit])
regretLog[i,]$Causal.notfound <- sum(estimate$Causal[-(1:SNP_edit_limit)])
regretLog[i,]$Fraction.random <- sum(estimate$Causal!=0) / SNP_candidates ## base rate: random guessing
regretLog[i,]$Fraction.causals <- round(regretLog[i,]$Causal.found / (regretLog[i,]$Causal.found+regretLog[i,]$Causal.notfound), digits=2)
regretLog[i,]$Regret <- (sum(estimate$Effect) - sum(estimate$Effect[1:SNP_edit_limit])) * SNP_mean_frequency
regretLog[i,]$N <- nrow(d)
regretLog[i,]$N.eff <- nrow(dAvailable)
if(verbose) { print(regretLog[i,]) }
}
qplot(regretLog$N, jitter(regretLog$Regret), xlab="Total N (not effective N)", ylab="Regret (expected lost IQ points compared to omniscience)", main=paste("Edits:", SNP_edit_limit, "; Candidates:", SNP_candidates)) + stat_smooth()
b <- BGLR(d$IQ.measured, ETA=list(list(X=d[-c(1, 2, length(colnames(d)))], model="BL", type="beta", probIn=0.12, counts=162, R2=r2, lambda=202, max=500)), verbose=FALSE)
means <- b$ETA[[1]]$b; sds <- b$ETA[[1]]$SD.b; qplot(SNP_effects, b$ETA[[1]]$b, color=b$ETA[[1]]$SD.b, main=paste("Edits:", SNP_edit_limit, "; Candidates:", SNP_candidates))
image(as.matrix(d[-c(1, 2, length(colnames(d)))]), col=heat.colors(2))