Rare Greek Variables
I scrape Arxiv to find underused Greek variables which can add some diversity to math; the top 10 underused letters are ϰ, ς, υ, ϖ, Υ, Ξ, ι, ϱ, ϑ, & Π. Avoid overused letters like λ, and spice up your next paper with some memorable variables!
Some Greek alphabet variables are just plain overused. It seems like no paper is complete without a bunch of E or μ or α variables splattered across it—and they all mean different things in different papers, and that’s when they don’t mean different things in the same paper! In the spirit of offering constructive criticism, might I suggest that, based on Arxiv frequency of usage, you experiment with more recherché, even, outré variables?
Instead of reaching for that exhausted π, why not use… ϰ (variant kappa), which looks like a Hebrew escapee? Or how about ς (variant sigma), which is calculated to get your reader’s attention by making them go “ςςς” and exclaim “these letters are Greek to me!” If that is too blatant, then I can recommend the subtle use of Υ (capital upsilon) instead of ‘Y’, which few readers will notice—but the ones who do, the hard way, will be asking themselves, “Υ‽ would any jury in the world convict me…?”
The top 10 least-used Greek variables on Arxiv, rarest to more common:
Quickly skimming papers on Arxiv, the equations often run together. It doesn’t help that everyone seems to overuse the same handful of Greek letters for everything, which rather defeats the point. Wouldn’t it be better if authors used variables which were a little unique, and we could enjoy the wonders of expressions like dividing a variable by its estimate, or as Eric Neyman would write it (inspired by Serge Lang), ?
First, though, we’d need to know which variables are underused—we can see which ones are overused, but it’s harder to see what ones are neglected. To estimate the frequency of variable use in scientific papers, I did some ad hoc parsing of Arxiv; this is a good proxy for STEM research in general, and because Arxiv is TeX-centric, it’s easy to parse out Greek variables with reasonable accuracy.
Data

Results.
Dataset: The Pile. The Arxiv scrape I use was released as part of the large 2020 text dataset The Pile; the shadowy hacker group known as EleutherAI scraped Arxiv in 2020 and converted it to a Markdown+TeX format, to simplify away the enormous amounts of TeX boilerplate while leaving the equations/variables. The Arxiv subset is provided as a 17GB tarball, 59GB uncompressed; it has 1.26m files with 417.6m lines / 7.2b words / 60.2b characters:
# if The Eye is down, use the torrent:
# https://academictorrents.com/details/0d366035664fdf51cfbe9f733953ba325776e667/tech
wget \
'https://the-eye.eu/public/AI/pile_preliminary_components/2020-09-08-arxiv-extracts-nofallback-until-2007-068.tar.gz'
tar xf '2020-09-08-arxiv-extracts-nofallback-until-2007-068.tar.gz'
cd ./documents/
find . -type f | wc --lines
# 1264405
find . -type f | xargs -n 9000 cat | wc
# 417,626,335 7,819,609,303 60,267,810,641To quickly visualize this dump, here’s 100 random lines from 1,000 random files:
find . -type f | shuf | head -1000 | xargs cat | shuf | head -100
# \end{array}
# Zeldovich Pancake
# {\begin{pmatrix}
# \kappa_{11}(I_r) - \kappa_{11}(\Omega \setminus I_r) \\
# If $G$ is a ‘blown-up’ $C_7$, then it is clearly $3$-colourable (as false twins can use the same color). Thus, Claim \[cl:c7\] enables us to assume $G$ has a cycle $C$ of length $5$, say its vertices are $c_1, c_2, c_3, c_4, c_5$, in this order. From now on, all index operations will be done modulo $5$. Because $G$ has no triangles, the neighbourhood $N_C$ of $V(C)$ in $G$ is comprised of 10 sets (some of these possibly empty):
#
# \end{aligned}$$
# [^1]: Note that in contrast to Logic Programming conventions, queries are not denoted by denials.
# )}{\bar{n}_{m}(\omega)}e^{-i\left( \nu-\omega\right) \left( \tau-t\right)
# \mathcal{M}_\beta\mathcal{K}^1_{-c}(\xi)&
# &=
# 512 3.50e$-$02 1.91 1.01e$-$01 1.11 2.57e$-$02 1.93 1.52e+02 1.04 1.65e$-$02 1.95
#
# \mathbf{Q}\left(\alpha\right)^{-1} \otimes \boldsymbol{\Sigma}_{jk} & \mathbf{Q}\left(\alpha\right)^{-1} \otimes \boldsymbol{\Sigma}_{jj} \notag
# $ 58243.6877674 $ & $ 32.9314 $ & $ 0.0070 $ & $ -0.005 $ & $ 0.010 $ & FEROS\
# So our restricted Schubert variety is in the affine space $\operatorname{Spec}(A')$ where $$A'=\operatorname{Sym}({\mathfrak{g}}_1) = \operatorname{Sym}(\bigwedge^3 F\oplus\bigwedge^2F\otimes G\oplus F\otimes\bigwedge^2 G).$$
# ✱✱Proof✱✱ First note that $$Q({S}_l({\mathcal A})) = \sum_{u \in \partial S_l({\mathcal A})} \pi(u)$$ and $$Q(\Omega \setminus {S}_l({\mathcal A})) = \sum_{u \in \partial S_l({\mathcal A})} \pi(u).$$ Further, $$\begin{aligned}
#
#
#
# ✱✱Keywords✱✱: Dilute suspensions, Eulerian models, direct and large eddy simulations, slightly compressible flows, dam-break (lock-exchange) problem.\
# We have the following corollary.
# Acknowledgements {#acknowledgements .unnumbered}
#
#
# \frac{\Xi_c^{(',✱)+}}{\sqrt{2}} &\frac{\Xi_c^{(',✱)0}}{\sqrt{2}} &\Omega_c^{(✱)0}
#
# (-1)^{p(i)} \lambda_{i} -\sum_{k=1}^{i-1}(-1)^{p(k)}
# (N,\varrho_L,\varrho_R)$, and acting on the morphisms as the identity map. The identities $G_L \circ G_R^{-1}=U$ and $G_R \circ G_L^{-1}=V$ prove that $U$ and $V$ are mutually inverse isomorphisms, as stated.
#
# 0 \mathop{\to}^\alpha - \eqspace + \mathop{\to}^\beta 0\eqspace (i=N)\;.$$ Note that all dynamical rules, conserving and non-conserving, are CP-symmetric, namely symmetric under the exchange of positive-negative charges and left-right directions. Generalizations of this model to the case were both types of particles can move in both directions, and when the dynamical rules break the CP symmetry, will be considered elsewhere.
# {#section-19}
# \[alg machine\]
# \bar{u}_j \pa_j \, \l \nonumber \\
#
# title: 'The Synthetic-Oversampling Method: Using Photometric Colors to Discover Extremely Metal-Poor Stars'
# 9 5 (1764,567,525,266,150,132,49,27,8,1) (1,1,2,2,1,1,2,2,1,1) 39204
#
# \nonumber\end{aligned}$$ Only $u$ and $du$ must be stored, resulting in two storage units for each variable, instead of three storage units for equation (\[s1\]). The third order nonlinearly stable version we use, Gottlieb & Shu (1998), has $m=3$ in (\[s2\]) with $$\begin{aligned}
# We inherit the notation of §\[SectionDModules\]. We begin with proving an explicit version of \[thm:mainDresult\]. Let $Y$ be a smooth product variety $Y=X\times Z$, $X$ be Affine and let $M=(E,\nabla)$ be a (meromorphic) integrable connection on $Y$. We denote $\pi_Z:Y\rightarrow Z$ the canonical projection. We revise the explicit ${\mathcal{D}}_Z$-module structure of $\int_{\pi_Z}M$. We can assume that $Z$ is Affine since the argument is local. From the product structure of $Y$, we can naturally define a decomposition $\Omega_{Y}^1(E)=\Omega^1_{Y/X}(E)\oplus\Omega^1_{Y/Z}(E)$. Here, $\Omega^1_{Y/X}(E)$ and $\Omega^1_{Y/Z}(E)$ are the sheaves of relative differential forms with values in $E$. By taking a local frame of $E$, we see that $\nabla$ can locally be expressed as $\nabla=d+\Omega\wedge$ where $\Omega\in\Omega^1(\operatorname{End}(E))$. We see that $\Omega$ can be decomposed into $\Omega=\Omega_x+\Omega_z$ with $\Omega_x\in \Omega^1_{Y/Z}(\operatorname{End}(E))$ and $\Omega_z\in \Omega^1_{Y/X}(\operatorname{End}(E))$. Then, $\nabla_{Y/Z}=d_x+\Omega_x\wedge$ and $\nabla_{Y/X}=d_z+\Omega_z\wedge$ are both globally well-defined and we have $\nabla=\nabla_{Y/X}+\nabla_{Y/Z}$. Here, $\nabla_{Y/X}:\mathcal{O}_{Y}(E)\rightarrow\Omega^1_{Y/X}(E)$ and $\nabla_{Y/Z}:\mathcal{O}_{Y}(E)\rightarrow\Omega^1_{Y/Z}(E)$. Note that the integrability condition $\nabla^2=0$ is equivalent to three conditions $\nabla_{Y/X}^2=0, \nabla_{Y/Z}^2=0,$ and $\nabla_{Y/X}\circ\nabla_{Y/Z}+\nabla_{Y/Z}\circ\nabla_{Y/X}=0$. For any (local algebraic) vector field $\theta$ on $Z$ and any form $\omega\in\Omega_{Y/Z}^✱(E)$, we define the action $\theta\cdot \omega$ by $\theta\cdot \omega=\iota_\theta(\nabla_{Y/X}\omega)$, where $\iota_\theta$ is the interior derivative. In this way, ${\rm DR}_{Y/Z}(E,\nabla)=(\Omega^{\dim X+✱}_{Y/Z}(E),\nabla_{Y/Z})$ is a complex of ${\mathcal{D}}_Z$-modules. It can be shown that ${\rm DR}_{Y/Z}(E,\nabla)$ represents $\int_{\pi_Z}M$ ([@HTT pp.45-46]).
#
# \
#
# \widehat{m}_{a}$$ or, using the rescaled $u_{B}$ to the conventional Bondi $u_{c}$ coordinate\[convention\][@coorTransf], by $u_{B}=\frac{u_{c}}{\sqrt{2}}$.
# Let $G=GL(m,n)$ and $B$ be the subgroup of upper triangular matrices. Then $\Lambda^+-\rho$ coincides with the set of dominant weights. Moreover, it is well-known (see for example [@P]) that for any $\lambda\in\Lambda^+$, $\Gamma_i(G/B,C_\lambda)=0$ if $i>0$. Moreover, $$\Gamma_0(G/B,C_\lambda)\simeq K_\lambda:=U({\EuFrak{g}})\otimes_{U({\EuFrak{g}}^+)}L_\lambda^0,$$ where ${\EuFrak{g}}^+={\EuFrak{g}}_0+{\EuFrak{b}}$ and $L_\lambda^0$ is the irreducible ${\EuFrak{g}}_0$-module of highest weight $\lambda$ with trivial action of ${\EuFrak{b}}_1$. The module $K_\lambda$ was first considered in [@Krep] and is usually called a Kac module. It was proven in [@Z] that every indecomposable projective module $P_\lambda$ has a filtration by Kac modules $K_\mu$ and that the multiplicity of $K_\mu$ in $P_\lambda$ equals the multiplicity of $L_\lambda$ in $K_\mu$. A combinatorial algorithm for calculating $a(\lambda,\mu)$ in this case was obtained by Brundan, [@B]. We will explain it in Section \[wd\] after introducing weight diagrams.
# Let $r = 1 + \frac{q}{p'}$. These two corollaries also imply that the A${}_r$ characteristic of each $|W^{-\frac{1}{q}} {\ensuremath{\vec{e}}}|^{p'}$ is bounded by ${\ensuremath [W]_{\text{A}_{p,q}}}^{r' - 1} $.
#
# The photocatalytic material is immersed in a solution of hydrogen peroxide fuel H$_2$O$_2$. Under activation by light, it decomposes the hydrogen peroxide fuel and the concentration profile of hydrogen peroxide, $[H_2O_2]_{(r, t)}$, is given by the solution of the diffusion-reaction equation: $$\partial_t [H_2O_2]_{(r, t)}= D^{\star}\Delta [H_2O_2]_{(r, t) } - \alpha [H_2O_2]_{(0, t) }
#
# 2.1. Single-machine scheduling with a common due window assignment [@jana04; @mos10b; @yeu01]
# \ln\mathcal{Z}=\frac{S}{2}\left[\frac{1}{Da_z}\ln\left
#
# G. Paltoglou, M. Theunis, A. Kappas, and M. Thelwall. Prediction of valence and arousal in forum discussions. submitted to [✱Journal of IEEE Transactions on Affective Computing✱]{}.
# M. Stoll. Implementing 2-descent for [J]{}acobians of hyperelliptic curves. , 98(3):245--277, 2001.
# $. In terms of the new variable $x$, Eq. (\[schrodinger1\]) is recast in the “Schrödinger-like” form $$\label{schrodinger2}
# --------------------
# \sum_{\beta=1}^{\alpha} \frac{1}{\omega(r_\beta)}.
# Наконец, если символ Сегре равен $[(1, 1), (1, 1), 1, 1]$, то $X$ содержит 4 особые точки. Они не лежат на одной плоскости, что видно из уравнений $X$, см. следствие \[sled1\]. Рассмотрим проекцию из трёхмерного проективного пространства, порождённого этими точками. Мы получаем $G$-эквивариантное расслоение над $\mathbb{P}^{1}$ на рациональные поверхности, являющиеся пересечиями двух квадрик. Применив эквивариантное разрешение особенностей расслоения, а затем эквивариантную относительную программу минимальных моделей, мы получим $G$-расслоение Мори на коники или поверхности дель Пеццо.
# Using independence statistic for Two-Sample Testing {#using-independence-statistic-for-two-sample-testing .unnumbered}
# \frac12 \bigl\| T_{\underline{\cZ}} P'_{\underline{\cB}|\underline{\cZ}} - P_{\underline{\cB}\underline{\cZ}} \bigr\|_1 \leq \epsilon_0 + \sum_{j=1}^m 2\epsilon_j.$$
#
# This paper reports that a simple particle filter applied to data on a time sequence has the ability of real-time decision making in the real world. This particle filter is named PFoE (particle filter on episode). Particle filters[@gordon1993] have been successfully applied to real-time mobile robot localization as the name [✱Monte Carlo localization✱]{} (MCL)[@dellaert1999; @fox2003]. MCLs are mainly applied in the state space of a robot, while PFoE is applied in the time axis. This paper shows some experimental results. The robot performs some teach-and-replay tasks with PFoE in the experiments. The tasks are simple and could also be handled by some deep neural network (DNN) approaches[@hirose2018; @pierson2017]. However, unlike DNN, the particle filter generates motions of robots without any learning phase for function approximation. Moreover, unlike MCL, it never estimates state variables directly. This phenomenon has never been reported.
# [^12]: This result is roughly consistent with the subsequent, similar analysis of @Choudhury15; however, here we only take the results from the former work as the latter does not provide statistically-quantitative constraints nor does it account for uncertainties in the ionising background.
#
# Define $m_{\alpha,n}:=m_{\alpha,n,w}= \max\{1,\lceil \alpha - w - 2bn\rceil\}$, in particular $\alpha \le m_{\alpha,n}+w+2bn$. We split (\[eq:add2\]) into two subsums: $\sum_{m_{\alpha,n}\le m\le M}$ and $\sum_{1 \le m< m_{\alpha,n}}$ (the splitting of the sum is because the general function $h(z,w):=\int_0^1 t^z\exp(wt)\,dt$ behaves essentially differently according to whether $|w|<|z|$ or $|z|<|w|$). Each term in the subsum $\sum_{m_{\alpha,n} \le m\le M}$ can be calculated explicitly as
#
#
# \right)^2$ of the flat direction. For $v \sim 10^{16}$ GeV, we expect this to be comparable to the (mass)$^2$ due to the inverted hierarchy which is $\sim -F_v^2 /v^2 \; d^2 Z(v)/ d (\ln v)^2$. It turns out that in this case the SUGRA contribution is smaller (by a factor of $\sim 4$) than the (mass)$^2$ due to the inverted hierarchy. This results in a shift of the minimum of $v$ by $\sim O(1/4) \;v$.
#
#
# eno.x & 999 & 999 & 98486.1688\
# bibliography:
# When we switch on the dephasing, $R_3$ stays a good entanglement measure unlike the von Neumann and Rényi entropies. In the open system, $R_3$ undergoes a characteristic stretched exponential decay starting at time scales $\gtrsim 1/\Gamma$ as shown in Fig. \[fig:sc\_exp\]. Such a decay can be understood as a superposition of local exponential decays, and has also been observed in the imbalance in Refs. [@Fischer2016; @Levi2016; @Everest2017] and is also experimentally confirmed [@Lueschen2017]. We observed such a decay as well in our exact simulations for other entanglement measures like the negativity and the Fisher information as we show in Appendix \[app:qfi\].
#
# \begin{array}{cc}
#
# t^\gamma|\varphi(t)|^p\,dt\bigg]^{1/p},$$ then the symbol $a(\xi)$ is called a Mellin $\mathbb{L}_{p,\gamma}$--multiplier.
# \tilde\omega^g_k\bigl(F_k(\phi_{tot})^2\bigr) &= \frac{1}{2},\end{aligned}$$ and the limit $k\to 0$ is trivial: $$F_0(n_{tot})=\lim_{k\to 0}F_k(n_{tot}) \quad\text{and}\quad
#
#
# [^7]: Note that there are many different nomenclatures throughout the machine-learning literature for the terms defined in Eqn. \[eq:precision\_recall\]. is most commonly referred to as the true positive rate (TPR), though it can also be referred to as the sensitivity, hit rate, or completeness depending on the context. I adopt the convention of referring to this as the as this is only discussed relative to the . The of a model is sometimes referred to as the positive predictive value or purity.
#
# \xi^{-1}(\hpart^\mu(\xi(f)\cdot_{U(\gg)}\xi(g))) =
# The states in Figs. \[strangemoms\](a) and \[strangemoms\](b) can be understood as the extreme limits of the states in Figs. \[moms\](d) and \[moms\](g), respectively.
# \sin v_{00}(t)
# M. Bredel and M. Fidler, “A measurement study regarding quality of service and its impact on multiplayer online games”, in ✱Proc. NetGames✱, 2010.
# Introduction and rational Arnoldi decompositions
# Our paper is organized as follows; in the next Section we discuss the changes that must be made in the nucleosynthesis code when neutrino heating is taken into account and how we implemented them. In the final Section, we discuss our numerical results, compare them to previous estimates for the change in $^4$He production, and finish with some concluding remarks.
# & & + \sum_{j} p(x_j^R) \ln p(x_j^R)
# \left( {1 \over D-3} - 1.13459 \right) \Lambda^{4+2(D-3)} \,.
# The Boroson and Green (1992, BG92) “Eigenvector 1” (EV1) is one of the reasons NLS1 are interesting, and why we are having a meeting about them. EV1 (also called Principal Component 1) is a linear combination of correlated optical and X-ray properties representing the greatest variation among a set of spectra. EV1 links narrower (BLR) H$\beta$ with stronger H$\beta$ blue wing, stronger FeII optical emission, and weaker \[OIII\]$\lambda 5007 emission from the NLR, with steeper soft X-ray spectra (Laor et al 1994, 1997). The narrower H$\beta$ defining NLS1s has been suggested to result from lower Black Hole masses, and therefore higher accretion rates relative to the Eddington limit in these luminous AGN. The NLS1s’ steep X-ray spectra are also suggested to tie in with high Eddington accretion rates (eg. Laor, these proceedings).
# To get the theorem, a spin structure is not necessary on $M$: any second order operator of the Laplace type with values on a vector bundle $V$ over $M$ (see [@Vassilevich:2003xt eq. (2.1)]) can replace ${\mathcal{D}}^2$.
#
# Following the notation of Eqn. (\[dl\]) we set up the following GP for $w$: $$w(u)\sim {\rm GP}(-1,K(u,u')).
# &\propto \exp\bigg\{-\frac{1}{2}\Big[\boldsymbol{\beta}^T \left\{\mathbf{X}\left(\boldsymbol{\theta}\right)^T\boldsymbol{\Omega}^{-1}\mathbf{X}\left(\boldsymbol{\theta}\right) + \mathbb{C}_{k|j}^{-1}\right\}\boldsymbol{\beta}\\
#
#
# title: |We can see that the Greek variables are often run-together, not delimited by anything except backslashes or punctuation (which begin/end TeX commands), whitespace is chaotic, and so on. Parsing the TeX into an AST or pulling apart expressions like \sum/\prod is right out1, but fortunately, that’s enough structure for our purposes: gauging overall letter use.
Parsing
Here I managed to use all the Greek letters—24.
John Nash, 200026ya?, on writing “Non-Cooperative Games” (used in A Beautiful Mind)
Split, sort, count, recount. The usual CLI strategy for counting histograms is to split into newline-delimited instances, sort, count, and resort by count. To look at the frequency of top-1000 ‘words’, I:
catall the files in parallelgrepfor math-related lines which contain a dollar sign or backslash, indicating TeXSplit lines at every backslash using
sed(preserving the backslash)Split lines at all whitespace and punctuation characters aside from backslash, using
tr(deleting those delimiters)I don’t do this in a single step using the
[:punct:]regexp character class, because that would delete the backslashes, which we want to keep.sortthe resulting lines, each of which should be a single ‘word’Count the runs of words using
uniq, producing n/word pairssortagain, to produce an ascending countTake the 1,000 most common words at the
tailof the output.
find . -type f | xargs -n 9000 cat | grep -F -e '$' -e '\' | tr '$' '\n' | sed -e 's/\\/\n\\/g' | \
tr "[:space:]\!\'#S%&(\)*+,-./:;<=>?@[/]^_{|}~" '\n' | \
sort | uniq --count | sort --numeric-sort | tail -n 1000
# 8499 details
# 8513 strongly
# 8571 \dim
# 8592 sense
# 8592 shape
# 8593 taking
# 8623 few
# 8642 estimates
# 8662 observe
# 8666 maximal
# 8671 half
# 8671 thermal
# 8679 events
# 8687 characteristic
# 8692 ec
# 8697 extended
# 8708 depend
# 8740 simply
# 8745 dual
# 8750 describe
# 8753 tree
# 8763 control
# 8764 inner
# 8771 \pm0
# 8776 processes
# 8781 nodes
# 8784 better
# 8784 identity
# 8789 regular
# 8791 profile
# 8794 performance
# 8814 35
# 8823 chain
# 8840 60
# 8851 pressure
# 8869 clusters
# 8875 gap
# 8889 samples
# 8891 quark
# 8899 convergence
# 8924 hole
# 8935 easily
# 8939 square
# 8968 \vartheta
# 8973 spaces
# 8979 off
# 9005 performed
# 9008 configuration
# 9023 regime
# 9038 27
# 9065 determine
# 9065 including
# 9085 satisfying
# 9089 introduce
# 9092 dashed
# 9109 coefficient
# 9112 \xspace
# 9120 odd
# 9130 decomposition
# 9146 what
# 9152 short
# 9202 another
# 9208 Given
# 9217 rank
# 9229 global
# 9260 presence
# 9269 experiments
# 9275 pairs
# 9280 exactly
# 9287 introduced
# 9288 figure
# 9289 \R
# 9291 conclude
# 9297 allows
# 9301 constraints
# 9310 denoted
# 9310 Indeed
# 9312 eff
# 9324 notation
# 9349 equilibrium
# 9351 45
# 9366 blue
# 9366 interval
# 9373 latter
# 9380 ds
# 9401 directly
# 9404 minimal
# 9405 required
# 9412 \vee
# 9419 entropy
# 9427 in
# 9440 norm
# 9444 02
# 9463 volume
# 9472 assumed
# 9477 period
# 9482 Fe
# 9488 relations
# 9495 images
# 9512 together
# 9516 already
# 9516 solid
# 9541 apply
# 9542 vectors
# 9552 angular
# 9558 features
# 9566 spatial
# 9606 energies
# 9622 computed
# 9626 leading
# 9629 luminosity
# 9642 various
# 9654 masses
# 9670 infinite
# 9673 existence
# 9688 studied
# 9696 measurement
# 9714 rather
# 9723 \bigr
# 9763 transformation
# 9772 Consider
# 9790 First
# 9802 interactions
# 9803 \bigl
# 9837 choose
# 9849 weight
# 9850 layer
# 9894 With
# 9921 increases
# 9932 procedure
# 9942 satisfy
# 9961 eqn
# 9975 family
# 10004 calculation
# 10006 clear
# 10016 Furthermore
# 10016 increase
# 10029 integer
# 10077 tab
# 10078 center
# 10092 panel
# 10095 coordinates
# 10112 significant
# 10115 Lemma
# 10123 compute
# 10154 dependent
# 10161 according
# 10181 provide
# 10190 Table
# 10202 simulation
# 10209 photon
# 10235 \sup
# 10276 scaling
# 10283 \cong
# 10283 say
# 10284 \dfrac
# 10315 magnitude
# 10352 fraction
# 10388 module
# 10397 II
# 10445 ab
# 10496 again
# 10502 during
# 10526 05
# 10532 construction
# 10532 written
# 10547 \hbox
# 10554 manifold
# 10557 ground
# 10578 subset
# 10645 GeV
# 10653 pdf
# 10655 best
# 10687 input
# 10700 per
# 10706 prop
# 10721 calculations
# 10742 \leqslant
# 10749 increasing
# 10764 physical
# 10772 always
# 10778 series
# 10781 minimum
# 10797 loop
# 10798 account
# 10815 ection
# 10823 proposed
# 10854 trivial
# 10855 make
# 10888 just
# 10893 channel
# 10905 comparison
# 10907 stable
# 10916 distributions
# 10924 chosen
# 10939 galaxy
# 10978 resolution
# 11000 methods
# 11000 scheme
# 11003 resulting
# 11017 test
# 11019 objects
# 11036 end
# 11039 almost
# 11060 numbers
# 11070 enough
# 11101 \longrightarrow
# 11108 \mapsto
# 11117 differential
# 11127 central
# 11139 exist
# 11151 before
# 11168 motion
# 11180 loss
# 11195 modes
# 11201 direct
# 11233 Gaussian
# 11251 optimal
# 11298 32
# 11304 groups
# 11330 good
# 11338 edges
# 11354 experimental
# 11391 formation
# 11393 polynomial
# 11395 addition
# 11395 arbitrary
# 11407 additional
# 11417 cm
# 11428 angle
# 11473 several
# 11484 An
# 11485 reduced
# 11491 Theorem
# 11512 unit
# 11514 law
# 11521 matrices
# 11535 amplitude
# 11556 diagram
# 11587 pmatrix
# 11590 expansion
# 11591 peak
# 11603 depends
# 11610 \star
# 11633 ph
# 11698 taken
# 11739 next
# 11859 true
# 11866 charge
# 11866 stellar
# 11886 applied
# 11887 leads
# 11890 disk
# 12017 axis
# 12020 natural
# 12023 yields
# 12045 cannot
# 12117 denotes
# 12160 19
# 12163 dynamics
# 12176 signal
# 12177 tensor
# 12207 choice
# 12225 unique
# 12230 \colon
# 12238 induced
# 12274 assumption
# 12284 Ref
# 12353 self
# 12355 \odot
# 12368 40
# 12383 2k
# 12404 presented
# 12470 regions
# 12490 optical
# 12501 domain
# 12530 still
# 12542 matter
# 12548 maps
# 12579 \bullet
# 12587 derived
# 12595 top
# 12614 discussed
# 12618 scalar
# 12643 exact
# 12647 background
# 12666 vertices
# 12695 max
# 12706 \min
# 12716 complete
# 12729 position
# 12747 measurements
# 12762 variable
# 12848 simulations
# 12860 write
# 12866 final
# 12882 however
# 12886 expression
# 12903 sources
# 12915 curves
# 12932 smooth
# 12933 When
# 12985 compact
# 12991 network
# 12997 \forall
# 13002 red
# 13012 Proposition
# 13064 path
# 13071 scattering
# 13090 normal
# 13101 uppose
# 13138 \hbar
# 13141 weak
# 13173 via
# 13211 eps
# 13219 connected
# 13281 open
# 13287 classical
# 13308 compared
# 13310 mode
# 13324 cluster
# 13352 01
# 13361 how
# 13365 inequality
# 13398 property
# 13412 close
# 13439 At
# 13474 lemma
# 13494 Finally
# 13560 last
# 13579 \lim
# 13581 numerical
# 13633 ii
# 13641 \bigg
# 13656 full
# 13700 23
# 13717 hep
# 13717 lem
# 13723 contribution
# 13777 critical
# 13821 Hamiltonian
# 13842 behavior
# 13854 long
# 13862 whose
# 13904 becomes
# 13917 them
# 13940 flow
# 13990 consistent
# 14017 de
# 14047 near
# 14047 negative
# 14116 less
# 14132 coefficients
# 14153 index
# 14176 Figure
# 14207 calculated
# 14208 24
# 14217 side
# 14235 One
# 14277 noise
# 14293 corresponds
# 14382 decay
# 14416 integral
# 14426 Our
# 14459 black
# 14460 gathered
# 14577 related
# 14611 correlation
# 14665 \textbf
# 14667 smaller
# 14714 contains
# 14740 symmetric
# 14797 \mid
# 14857 continuous
# 14862 information
# 14904 effects
# 14908 observations
# 14975 take
# 15030 span
# 15050 particles
# 15053 spectra
# 15108 band
# 15122 four
# 15128 give
# 15130 18
# 15135 times
# 15148 satisfies
# 15152 closed
# 15164 cross
# 15181 ray
# 15229 seen
# 15235 metric
# 15249 electron
# 15292 around
# 15340 100
# 15340 vertex
# 15380 radius
# 15393 \oplus
# 15399 direction
# 15406 plane
# 15412 dt
# 15440 fit
# 15457 variables
# 15461 further
# 15465 17
# 15497 pair
# 15510 sets
# 15544 formula
# 15556 relative
# 15593 measured
# 15593 Using
# 15611 dimension
# 15624 need
# 15635 arXiv
# 15675 means
# 15679 either
# 15680 \max
# 15681 maximum
# 15697 22
# 15767 bounded
# 15781 much
# 15796 change
# 15809 previous
# 15814 without
# 15829 50
# 15945 determined
# 15970 node
# 15997 generated
# 16005 dependence
# 16020 21
# 16037 step
# 16042 important
# 16074 \simeq
# 16137 Moreover
# 16141 \limits
# 16141 representation
# 16164 being
# 16177 spectral
# 16225 operators
# 16302 considered
# 16308 \displaystyle
# 16309 thm
# 16323 There
# 16354 basis
# 16367 30
# 16477 current
# 16539 difference
# 16620 evolution
# 16670 \wedge
# 16698 approximation
# 16727 product
# 16728 25
# 16739 \Vert
# 16798 upper
# 16801 expected
# 16803 sum
# 16807 From
# 16842 light
# 16852 strong
# 16858 hence
# 16902 many
# 16947 gauge
# 16977 components
# 16981 \perp
# 16995 \subseteq
# 17024 least
# 17061 equivalent
# 17150 2n
# 17168 \prod
# 17197 curve
# 17220 gas
# 17226 edge
# 17291 wave
# 17312 element
# 17426 momentum
# 17517 measure
# 17599 source
# 17647 flux
# 17747 frequency
# 17789 effective
# 17790 ection
# 17816 \ln
# 17826 after
# 17835 equal
# 17860 note
# 17896 solutions
# 17934 algorithm
# 17972 degree
# 18052 approach
# 18159 could
# 18164 interaction
# 18187 error
# 18373 \setminus
# 18460 galaxies
# 18510 \Pi
# 18536 systems
# 18552 invariant
# 18569 \hspace
# 18600 On
# 18639 average
# 18654 class
# 18723 lattice
# 18740 particle
# 18748 estimate
# 18761 called
# 18761 therefore
# 18789 ratio
# 18823 Now
# 18852 \ar
# 18943 dx
# 18954 definition
# 18963 described
# 18976 coupling
# 19073 transition
# 19158 like
# 19231 prove
# 19252 image
# 19298 theorem
# 19330 algebra
# 19365 symmetry
# 19383 complex
# 19385 holds
# 19403 emission
# 19522 \underline
# 19546 elements
# 19546 relation
# 19572 00
# 19652 effect
# 19691 \mathscr
# 19694 way
# 19696 random
# 19759 graph
# 19804 \dagger
# 19834 component
# 19892 star
# 19951 fields
# 19956 simple
# 19989 those
# 20038 larger
# 20065 Figure
# 20071 action
# 20075 study
# 20094 must
# 20131 \Theta
# 20359 \sin
# 20370 Hence
# 20421 \cup
# 20422 distance
# 20433 work
# 20653 sample
# 20756 real
# 20777 here
# 20806 stars
# 20849 length
# 20911 \exp
# 20977 \cos
# 20996 split
# 21005 gives
# 21035 These
# 21128 along
# 21194 known
# 21247 get
# 21289 through
# 21344 \approx
# 21364 independent
# 21375 associated
# 21396 14
# 21459 process
# 21473 main
# 21473 \textrm
# 21577 level
# 21620 standard
# 21848 velocity
# 21954 hand
# 22015 within
# 22059 mean
# 22081 power
# 22104 respect
# 22123 Here
# 22137 higher
# 22181 below
# 22364 about
# 22773 properties
# 22834 should
# 22896 new
# 22921 Lemma
# 22921 th
# 23040 do
# 23139 sequence
# 23225 lines
# 23226 spectrum
# 23250 factor
# 23409 free
# 23434 paper
# 23438 initial
# 23481 conditions
# 23563 analysis
# 23570 Phys
# 23572 surface
# 23690 boundary
# 23730 thus
# 23806 part
# 23854 present
# 24157 implies
# 24307 rate
# 24328 bound
# 24498 \neq
# 24590 quantum
# 24637 "fig
# 24639 fixed
# 24693 equations
# 24730 magnetic
# 24770 method
# 24780 size
# 24928 single
# 24939 \equiv
# 25002 \ast
# 25019 16
# 25112 lower
# 25138 \dot
# 25299 scale
# 25424 under
# 25495 denote
# 25529 total
# 25577 possible
# 25605 left
# 25810 operator
# 25839 20
# 25911 range
# 25995 found
# 26092 even
# 26159 assume
# 26160 \over
# 26208 13
# 26245 based
# 26344 region
# 26352 local
# 26358 Therefore
# 26675 positive
# 26861 define
# 26975 potential
# 26978 because
# 27291 probability
# 27352 they
# 27381 similar
# 27390 exists
# 27495 dimensional
# 27512 sec
# 27562 \ge
# 27616 now
# 27744 \mathsf
# 27806 condition
# 27848 up
# 28192 \qquad
# 28219 example
# 28231 does
# 28283 label
# 28354 low
# 28356 fact
# 28431 Note
# 28435 type
# 28517 would
# 28580 observed
# 28690 al
# 28767 find
# 28956 particular
# 28995 very
# 29072 right
# 29134 while
# 29279 models
# 29368 map
# 29371 15
# 29390 cases
# 29405 proof
# 29687 most
# 29795 due
# 29892 general
# 29984 term
# 30391 temperature
# 30515 every
# 30641 high
# 30648 \subset
# 30717 spin
# 30838 \cap
# 30846 limit
# 30862 out
# 31092 Theorem
# 31140 problem
# 31142 --
# 31450 linear
# 31506 us
# 31515 points
# 31626 three
# 31637 \Psi
# 31761 However
# 31840 second
# 31969 parameter
# 32722 vector
# 32811 group
# 33189 let
# 33192 theory
# 33458 were
# 33674 \cdots
# 33674 zero
# 33685 Thus
# 33714 ij
# 33902 shows
# 34336 \widehat
# 34471 "
# 34567 \dots
# 34575 structure
# 34663 respectively
# 34756 To
# 34866 solution
# 34951 o
# 35131 section
# 35341 states
# 35732 obtain
# 35743 parameters
# 35865 11
# 36171 By
# 36487 \vert
# 36520 functions
# 36902 et
# 36996 consider
# 37204 finite
# 37307 since
# 37471 phase
# 37618 corresponding
# 37695 constant
# 37896 terms
# 38056 their
# 39235 width
# 39439 no
# 39720 ince
# 40030 distribution
# 40445 obtained
# 40770 \Big
# 40961 \zeta
# 40991 been
# 41161 result
# 41278 \log
# 41852 line
# 42246 well
# 42691 \widetilde
# 43676 matrix
# 43771 may
# 43833 large
# 44000 \vec
# 44330 equation
# 44354 shown
# 44411 small
# 44523 use
# 45204 \circ
# 45781 \nabla
# 46149 both
# 46219 \prime
# 46255 show
# 46836 igma
# 47085 As
# 47317 Eq
# 47539 into
# 48207 above
# 48304 used
# 48583 \mbox
# 48915 density
# 48935 follows
# 49519 values
# 49938 \rightarrow
# 50333 value
# 50444 \big
# 50694 \sim
# 51078 12
# 51303 over
# 51406 array
# 51456 defined
# 51656 9
# 51829 different
# 52280 more
# 52379 \nonumber
# 52380 system
# 52427 \Phi
# 52573 \otimes
# 52761 mass
# 52834 \kappa
# 53074 when
# 53226 \Lambda
# 53241 but
# 53306 form
# 54001 \le
# 54100 If
# 54136 \chi
# 54217 point
# 54415 non
# 55102 was
# 55570 \geq
# 55712 \ldots
# 55720 its
# 55921 other
# 55963 \cal
# 56838 \bm
# 56888 \quad
# 56926 space
# 57632 some
# 57694 \mathfrak
# 57801 so
# 57989 same
# 58229 It
# 58933 following
# 59159 Then
# 59498 results
# 59776 state
# 62232 using
# 64068 fig
# 64744 first
# 65179 than
# 65837 number
# 65856 \ensuremath
# 66915 field
# 67707 Fig
# 68696 these
# 69927 \langle
# 70700 7
# 71141 any
# 71325 energy
# 71972 \varphi
# 72985 order
# 75413 \overline
# 75582 between
# 76547 \boldsymbol
# 76618 \bf
# 76930 \Gamma
# 77544 our
# 77558 \ell
# 78445 will
# 78597 given
# 78627 see
# 79390 set
# 79513 O
# 79537 there
# 79777 each
# 79923 model
# 80221 time
# 80862 8
# 82869 \varepsilon
# 82918 data
# 83545 \sqrt
# 83948 \epsilon
# 84045 \operatorname
# 84107 \Omega
# 85112 \eta
# 85813 only
# 86304 \to
# 87056 Let
# 88025 \pm
# 88504 \psi
# 90710 case
# 92247 also
# 96039 function
# 97447 or
# 98664 \rangle
# 98808 \xi
# 98973 \cdot
# 99039 then
# 100298 \text
# 101654 \tilde
# 102946 Y
# 103415 has
# 103613 \int
# 105087 W
# 105094 eq
# 106302 \bar
# 106454 For
# 106766 6
# 107048 \times
# 107669 \Delta
# 109607 \hat
# 109865 J
# 110180 10
# 110262 such
# 110570 Z
# 112395 This
# 114806 two
# 116924 \phi
# 117758 \infty
# 118872 if
# 119175 \nu
# 119641 Q
# 121016 \leq
# 122994 \omega
# 123281 \partial
# 124327 one
# 124865 w
# 127349 all
# 127677 \tau
# 131846 \theta
# 133824 not
# 133858 \delta
# 134144 \sum
# 139006 U
# 141176 l
# 141205 it
# 141646 \rho
# 149822 I
# 150294 \beta
# 155404 \mathrm
# 155919 \gamma
# 156210
# 160078 \pi
# 162781 \sigma
# 163904 h
# 168255 have
# 169312 \end
# 170128 5
# 170643 \begin
# 171324 K
# 171501 \label
# 172817 V
# 174296 where
# 182423 \mathbf
# 187751 \rm
# 190746 We
# 190825 \lambda
# 191058 In
# 193927 D
# 196419 G
# 198971 can
# 201043 an
# 203650 F
# 206193 which
# 207575 v
# 208740 \mu
# 214082 E
# 214573 q
# 215643 P
# 216188 \mathbb
# 218298 aligned
# 220590 b
# 221819 y
# 222123 z
# 224395 at
# 227080 g
# 228811 from
# 233845 this
# 234477 B
# 245972 u
# 250897 H
# 256360 c
# 260556 C
# 261210 L
# 263228 4
# 272451 X
# 273981 e
# 275675 f
# 278366 R
# 282860 M
# 282880 on
# 283442 \alpha
# 284669 N
# 297697 T
# 298949 r
# 300950 d
# 308799 s
# 316151 \in
# 320832 j
# 331567 as
# 332873 m
# 335739 \mathcal
# 344645 \right
# 344676 \left
# 345559 be
# 356318 p
# 369532 are
# 392620 A
# 405424 by
# 416861 The
# 429757 3
# 452133 \frac
# 459410 with
# 477713 we
# 507216 t
# 511949 k
# 626434 x
# 631460 for
# 651310 that
# 670505 n
# 688546 i
# 913220 to
# 1004108 in
# 1116686 is
# 1259044 0
# 1300391 and
# 1308407 a
# 1559082 2
# 1920268 of
# 2000582 1
# 3189037 \
# 3758226 the
# 64052776The results look plausible overall. We want to search that for the Greek alphabet specifically.2
Alphabet zoo. The TeX Greek alphabet is a little tricky. Several of the Greek letters come with variants which have the \var prefix. Who knew there’s a π variant, ϖ? (Not most Arxiv authors, turns out. At least the really obscure ones like ϡ & Ϙ aren’t supported at all and need not be considered.) And what’s up with digamma? Most letters are defined reasonably mnemonically with a lowercase and uppercase version, like \delta vs \Delta, but Knuth, in one of his overly-clever TeX design choices, leaves out cases where the English letter is ‘close enough’—eg there is no \Beta, you just have to know to type B instead (not to be confused with the Unicode version, which does distinguish, of course, and where ‘B’ ≠ ‘Β’). Epsilon, for example, both has a variant and an overloaded English uppercase, while omicron has neither lowercase nor uppercase and is just o/O!3
This complicates the search because we cannot simply match on backslash, and is one reason we split on punctuation and whitespace, which catches the English puns. We have to specify that we are matching the entire line: you cannot grep for ‘H’, you have to grep for the line being solely H, ^H$. And likewise for the others.
Counting
After compiling the list of 55 lowercase, variants, uppercase, and English lower/uppercase versions, we can grep and count as before:
find . -type f | parallel cat | grep -F -e '$' -e '\' | tr '$' '\n' | sed -e 's/\\/\n\\/g' | \
tr "[:space:]\!\'#%&(\)*+,-./:;<=>?@[/]^_{|}~" "\n" | \
grep -E -e '^\\alpha$' -e '^A$' \
-e '^\\beta$' -e '^B$' \
-e '^\\gamma$' -e '^\\Gamma$' \
-e '^\\delta$' -e '^\\Delta$' \
-e '^\\epsilon$' -e '^\\varepsilon$' -e '^E$' \
-e '^\\zeta$' -e '^Z$' \
-e '^\\eta$' -e '^H$' \
-e '^\\theta$' -e '^\\vartheta$' -e '^\\Theta$' \
-e '^\\iota$' -e '^I$' \
-e '^\\kappa$' -e '^\\varkappa$' -e '^K$' \
-e '^\\lambda$' -e '^\\Lambda$' \
-e '^\\mu$' -e '^M$' \
-e '^\\nu$' -e '^N$' \
-e '^\\xi$' -e '^\\Xi$' \
-e '^o$' -e '^O$' \
-e '^\\pi$' -e '^\\varpi$' -e '^\\Pi$' \
-e '^\\rho$' -e '^\\varrho$' -e '^P$' \
-e '^\\sigma$' -e '^\\varsigma$' -e '^\\Sigma$' \
-e '^\\tau$' -e '^T$' \
-e '^\\upsilon$' -e '^\\Upsilon$' \
-e '^\\phi$' -e '^\\varphi$' -e '^\\Phi$' \
-e '^\\chi$' -e '^X$' \
-e '^\\psi$' -e '^\\Psi$' \
-e '^\\omega$' -e '^\\Omega$' \
| sort | uniq --count | sort --numeric-sort
# 3097 \varkappa
# 4642 \varsigma
# 7268 \upsilon
# 9839 \varpi
# 11043 \Upsilon
# 17534 \varrho
# 19631 \Xi
# 19928 \vartheta
# 22412 \iota
# 51726 \Pi
# 53511 \Theta
# 66761 o
# 88417 \Psi
# 118005 \zeta
# 128748 \Sigma
# 139848 \kappa
# 159460 \Phi
# 164266 \chi
# 168868 \Lambda
# 205153 O
# 214174 \varphi
# 243244 \epsilon
# 245256 \varepsilon
# 248825 \Gamma
# 258733 \Omega
# 261916 \psi
# 267369 \eta
# 274331 \xi
# 320644 \Delta
# 331012 \nu
# 335777 Z
# 363178 \phi
# 378808 \theta
# 386587 \omega
# 389702 \tau
# 397955 \delta
# 400724 \rho
# 430456 I
# 438142 \gamma
# 464572 \beta
# 469976 \pi
# 498721 \sigma
# 527385 K
# 553494 \lambda
# 605726 P
# 620454 \mu
# 620883 E
# 683035 B
# 710857 H
# 787675 M
# 798170 X
# 811558 N
# 854002 T
# 854467 \alpha
# 1107994 AThe top 10:
A(Α)\alpha(α)T(Θ)N(Ν)X(Χ)M(Μ)H(Η)B(Β)E(Ε)\mu(μ)
The bottom 10:
\varkappa(ϰ)\varsigma(ς)\upsilon(υ)\varpi(ϖ)\Upsilon(Υ)\varrho(ϱ)\Xi(Ξ)\vartheta(ϑ)\iota(ι)\Pi(Π)
Distribution
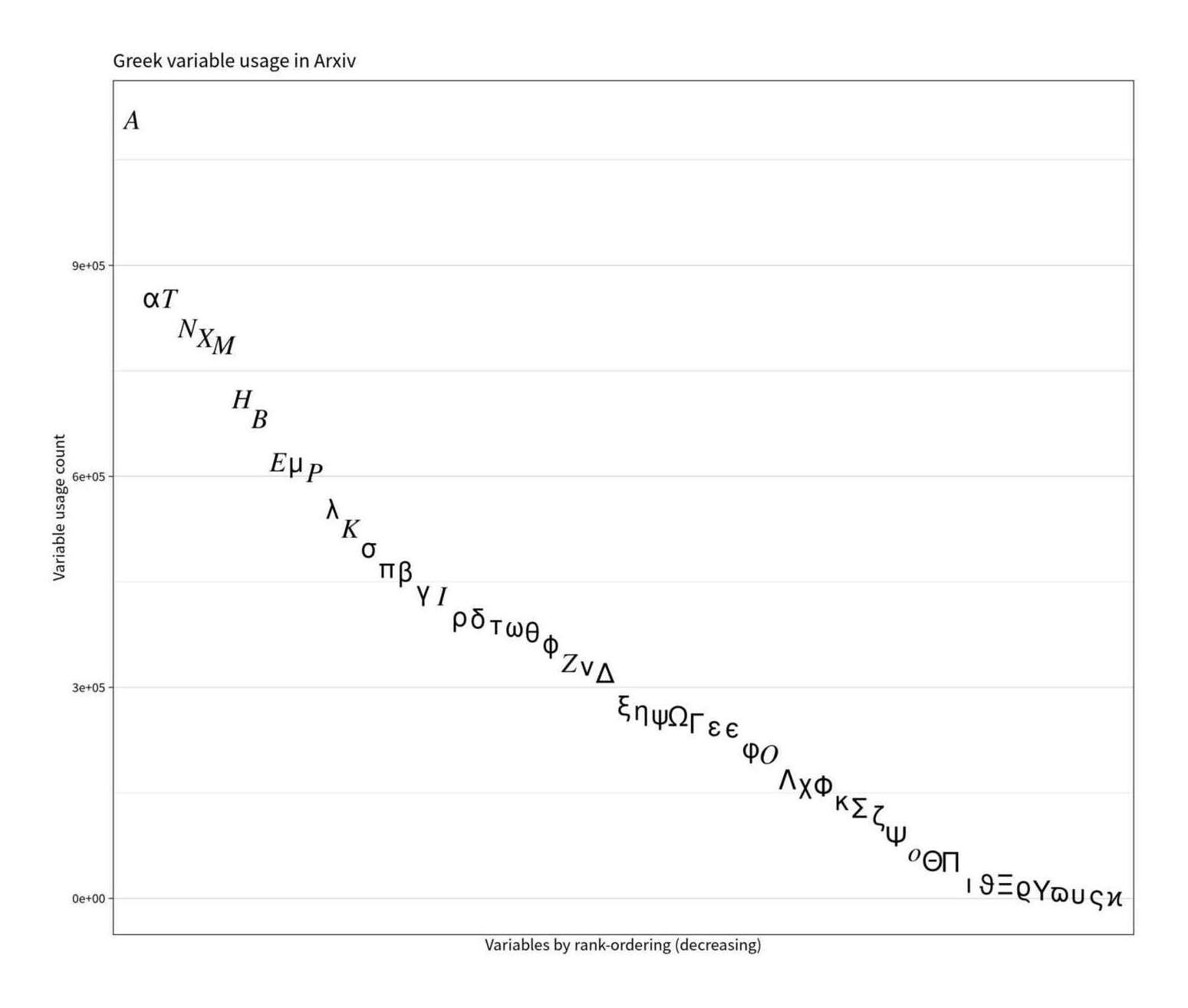
Distribution of Greek alphabet letter frequencies in Arxiv
frequency <- rev(c(3097, 4642, 7268, 9839, 11043, 17534, 19631, 19928, 22412, 51726, 53511,
66761, 88417, 118005, 128748, 139848, 159460, 164266, 168868, 205153,
214174, 243244, 245256, 248825, 258733, 261916, 267369, 274331, 320644,
331012, 335777, 363178, 378808, 386587, 389702, 397955, 400724, 430456,
438142, 464572, 469976, 498721, 527385, 553494, 605726, 620454, 620883,
683035, 710857, 787675, 798170, 811558, 854002, 854467,1107994))
round(digits=3, frequency / sum(frequency))
# [1] 0.060 0.046 0.046 0.044 0.043 0.042 0.038 0.037 0.033 0.033 0.033 0.030 0.028
# 0.027 0.025 0.025 0.024 0.023 0.022 0.021 0.021 0.021 0.020 0.020 0.018 0.018 0.017
# [28] 0.015 0.014 0.014 0.014 0.013 0.013 0.013 0.012 0.011 0.009 0.009 0.009 0.008
# 0.007 0.006 0.005 0.004 0.003 0.003 0.001 0.001 0.001 0.001 0.001 0.001 0.000 0.000
# [55] 0.000
library(ggplot2)
g <- qplot(1:length(frequency), frequency) +
xlab("Variables by rank-ordering (decreasing)") + ylab("Variable usage count") +
ggtitle("Greek variable usage in Arxiv") +
scale_x_discrete(expand = c(0.02,0)) + # reduce internal padding to minimize overlap
geom_text(size=I(14),
label=rev(c("ϰ", "ς", "υ", "ϖ", "Υ", "ϱ", "Ξ", "ϑ", "ι", "Π", "Θ", "𝑜", "Ψ", "ζ", "Σ",
"κ", "Φ", "χ", "Λ", "𝑂", "φ", "ϵ", "ε", "Γ", "Ω", "ψ", "η", "ξ", "Δ", "ν",
"𝑍", "ϕ", "θ", "ω", "τ", "δ", "ρ", "𝐼", "γ", "β", "π", "σ", "𝐾", "λ", "𝑃",
"μ", "𝐸", "𝐵", "𝐻", "𝑀", "𝑋", "𝑁", "𝑇", "α", "𝐴")))
g$layers[[1]] <- NULL ## delete the geom_text default layer
gThe distribution of usage looks like a smooth dropoff by rarity. Usually, these turn out to be something related to Zipf’s law; whether it’s a Pareto like natural language vocabulary, or something else (like a Poisson), this is probably too few items to test—it looks like one, but is too noisy to tell, perhaps due to inflation from my cheap error-prone parsing. et al 2024 analyzes physics equations more rigorously, and finds that the frequency of ‘operators’ (including functions like exponents or fundamental constants) seem Zipf-distributed.
‘Α’ anomalously popular. Most of the high-ranking variables are expected: of course \beta or \pi or \mu will be common. The spike/jump of Α is almost surely an unavoidable glitch from the ad hoc parsing: you can’t easily distinguish between ‘A’ which is being used in a normal English sentence (“… A good example…”), and ‘A’ which is in an TeX expression like “… + A + …”—that would require full parsing to understand whether it’s in a prose or formula context, and is not doable with shell scripting. (This applies less to the other capitals like E/B/X/O, which are generally not used isolated like Α is.)
‘Π’ anomalously unpopular. Perhaps unsurprisingly, the variants typically rank low, and there is enormous differences in frequency: the most common backslashed entity is 298× more common than the rarest. More puzzling are some of the low ones: given how incredibly common \pi is, why is its capital version \Pi so rare? (Are people shying away from it because Π—despite being much smaller—looks like the multiplication/product summation, which is itself usually written as \prod?) Is \iota really that rare?4 And what do people have against poor upsilon?