International population online surveys of cat owners about catnip and other cat stimulant use.
In compiling a meta-analysis of reports of catnip response rats in domestic cats, yielding a meta-analytic average of ~2⁄3, the available data suggests heterogeneity from cross-country differences in rates (possibly for genetic reasons) but is insufficient to definitively demonstrate the existence of or estimate those differences (particularly a possible extremely high catnip response rate in Japan). I use Google Surveys August–September 2017 to conduct a brief 1-question online survey of a proportional population sample of 9 countries about cat ownership & catnip use, specifically: Canada, the USA, UK, Japan, Germany, Brazil, Spain, Australia, & Mexico. In total, I surveyed n = 31,471 people, of whom n = 9,087 are cat owners, of whom n = 4,402 report having used catnip on their cat, and of whom n = 2996 report a catnip response.
The survey yields catnip response rates of Canada (82%), USA (79%), UK (74%), Japan (71%), Germany (57%), Brazil (56%), Spain (54%), Australia (53%), and Mexico (52%). The differences are substantial and of high posterior probability, supporting the existence of large cross-country differences. In additional analysis, the other conditional probabilities of cat ownership and trying catnip with a cat appear to correlate with catnip response rates; this intercorrelation suggests a “cat factor” of some sort influencing responses, although what causal relationship there might be between proportion of cat owners and proportion of catnip-responder cats is unclear.
An additional survey of a convenience sample of primarily US Internet users about catnip is reported, although the improbable catnip response rates compared to the population survey suggest the respondents are either highly unrepresentative or the questions caused demand bias.
Google Consumer Surveys/Google Surveys (GS) is an online survey service offered by Google to the general population; it is powered by media publishers where their article paywalls are replaced by a short typically single-question survey of a variety of types which the reader must answer to see the desired content. Combining metadata with Google’s advertising profiles, Google attempts to weight selected readers for the “surveywall” such that they form an unbiased random probability sample of a specified population, such as the general population. Each GS response costs $0.12$0.12017–$3.65$32017 depending on the length of the survey & difficulty of recruiting responses (eg. a country-wide all-ages all-gender probability sample survey with one question would cost $0.12$0.12017 per response, so $12.18$102017 would yield 100 answers).
As of August 2017, GS allows targeting:
-
by age bracket:
-
18–24
-
25–34
-
35–44
-
44–54
-
55–64
-
65+
-
-
gender: women/men
-
country (and by sub-country, specific regions depending on country):
-
United States (English)
-
Canada (English)
-
United Kingdom (English)
-
Germany (German)
-
Mexico (Spanish)
-
Japan (Japanese)
-
Australia (English)
-
Brazil (Portuguese)
-
France (French)
-
Spain (Spanish)
-
for Android smartphone readers only, Italy (Italian) and the Netherlands (Dutch but not English)
-
-
by predefined groups, “audience panels” (costing more, ≥ $0.37$0.32017); eg. for the United States, available audience panels include:
-
“Hispanics/Latinos”
-
“Online dating users (Sites and apps)”
-
“Small/Medium Business Owners and Managers”
-
“Mobile social media users (Facebook, Twitter, Google+)”
-
“Streaming video subscription users (Netflix, Amazon, Hulu Plus, Google Play)”
-
“Students”
-
-
by user-defined “screening question” which provides a conditional question, and one is charged only for the users who answer positively & proceed to the main survey question.
For catnip surveying, GS has advantages and disadvantages. The primary advantages are that a well-powered single-question survey about catnip response could potentially be cheap, while delivering an unbiased estimate from the general population uninterested in cats or catnip (particularly in Japan, given the Japanese anomaly in the initial meta-analysis), and incidentally measuring proportions that might also be of interest (such as international differences in cat ownership or familiarity with catnip). The disadvantages are that the cost advantage may be illusory as most respondents simply will not have a cat or will not have tried to use catnip (never mind any of the more obscure cat stimulants like silvervine), and the survey must be kept as simple as possible to keep respondents honest & costs down.
Given the screening question feature, a single-question catnip survey could be defined either as a 2-stage survey with a screening question asking about cat ownership and then results of catnip use if any, or as a single-question asking about catnip with the set of responses no-cat/cat-but-never-catnip/cat-and-response/cat-and-no-response. If half of Americans have a cat, and half of cat-owners have tried catnip, then one would need 4 responses for every useful response, so it would cost $0.49$0.42017/response. The screening question might be more efficient.
2017 Google Surveys: Probability Population Sample
Pilot Surveys
I experimented with 2 screening-question GS surveys, “Do you have a cat?” and “Have you ever given catnip to a cat?”; after its automatic pilot experiment, GS priced responses to both at $3.65$32017 each, which is unacceptably expensive. I then experimented with 2 single-question GS surveys, where the set of responses covers the 2×2=4 possibilities of cat ownership & catnip use, to see if they would be sufficiently cheap as to be more cost-effective after omitting the uninformative cells (of not owning a cat, and of owning a cat but never trying catnip).
The first GS survey was the straightforward single-question version to try to estimate what fraction of respondents would not have a cat & not have tried catnip, to see what the cost might be; the second reversed the responses to ask about catnip immunity rather than response, to try to reduce any demand bias:
-
2017-07-28–3d2017-07-30, 100 res$0.12$0.12017 = $12.18$102017, USA general population (raw responses)
-
Have you ever given catnip to your cat?
[randomized order]
-
No: I do not have a cat [n = 65 / 62%]
-
No: I have a cat but have not tried catnip [n = 12 / 16%]
-
Yes: but they did not respond to catnip [n = 6 / 5%]
-
Yes: they responded to catnip [n = 18 / 17%]
24 useful responses, implying a 25% immunity rate.
-
-
2017-07-29–4d2017-08-01, 200 res$0.12$0.12017 = $24.36$202017, USA general population (raw responses):
-
Have you ever given catnip to your cat?
[randomized order]
-
No: I do not have a cat [n = 136 / 72%]
-
No: I have a cat but have not tried catnip [n = 19 / 9.9%]
-
Yes: and they were catnip-immune [n = 11 / 4.7%]
-
Yes: but they were not immune [n = 34 / 13.3%]
45 useful responses, implying a 24% immunity rate.
-
-
combined, n = 300:
-
No cat: n = 201 / 67%
-
Cat but no tries: n = 31 / 10%
-
Cat and tried: n = 69 / 23%; result:
-
none/immune: n = 17 / 24%
-
responder: n = 52 / 75%
-
-
Pooling, about 1 in 7 or 15% ((34+11)/(100+200) = 34⁄300 = 0.15) of the responses were useful, so the true cost of one response was ~$0.82$0.672017; so the screening question survey would cost 4.5× more than the single-question version. (Google Surveys sometimes errs on the side of collecting too many responses, but does not appear to charge you for the excess, so the cost-effectiveness will be better than appears.) Demand bias wise, the proportions are identical between the normal & negated responses, providing some evidence that respondents are not mindlessly responding.
Combining the pilot survey samples and comparing with the earlier meta-analytic estimate of 63% response rate / 37% immunity observed in lab animals/research settings, the difference would be just statistically-significant when ignoring the meta-analytic uncertainty (binom.test(c(17, 52), p=0.37) → p = 0.034, CI 0.15–0.365), so it may be the case that the cat owners are more likely to say their cat responds to catnip This could be seen as a good or bad thing: there might be demand bias or selective memory where respondents think more of catnip-responders, or it could be that cat owners are inherently better judges of their cats’ responses because they are familiar with the cats in question, the cats are comfortable with the owners providing the catnip, and owners likely try catnip on multiple occasions to observe if any response is ever elicited (whereas in a laboratory setting, all of these variables are reversed in a way that would tend to hide catnip responses: the investigator may not be familiar with or good at handling the cat, the cat may be scared of them or the lab setting, and most studies report only 1 test occasion despite responders not always responding & requiring multiple tests to be sure).
Full International Surveys
This difference, and the apparent success of the pilot survey, suggests the need for a larger survey sample to nail down the estimate more accurately, and exploit the ability to sample other countries (especially Japan). To sample all 9 non-US countries (omitting Italy & the Netherlands because of the unknown biases in sampling only Android smartphone users), I will need translations of the questions into: French, German, Japanese, Portuguese, & Spanish.
International Survey Results
Results by country (note that percentages do not equal raw counts due to population weighting; original Excel spreadsheet exports):
-
Canada: 2017-08–07-2017-08-14, 3000 responses × $0.12$0.12017 = $365.33$3002017, Canada general population (raw responses)
-
Have you ever given catnip to your cat? [n = 3001]
[randomized order]
-
No: I do not have a cat [n = 193886ya / 63%]
-
No: I have a cat but have not tried catnip [n = 260 / 9%]
-
Yes: but they did not respond to catnip [n = 139 / 5.3%]
-
Yes: they responded to catnip [n = 664 / 23%]
139⁄803 = 17% immunity rate. Canadians appear more likely to have cats, try catnip, and receive a catnip response.
-
-
Canada: 2017-08-19–4d2017-08-22, 150 resraw responses); adaptive sampling followup:
-
no: 99 (62%)
-
non-trier: 12 (9.5%)
-
non-response: 8 (5.9%)
-
response: 31 (23%)
8⁄31 = 25.8% immunity rate.
-
-
Australia: 2017-08-07–4d2017-08-10, 3000 res$0.12$0.12017 = $365.33$3002017, Australia general population (raw responses)
-
Have you ever given catnip to your cat? [n = 3000]
[randomized order]
-
No: I do not have a cat [n = 2134 / 71%]
-
No: I have a cat but have not tried catnip [n = 446 / 14.3%]
-
Yes: but they did not respond to catnip [n = 196 / 6.8%]
-
Yes: they responded to catnip [n = 224 / 7.7%]
196⁄420 = 47% immunity rate. This is surprisingly high: almost twice the US/UK estimates even though one would expect that Australian rates would be similar as it was colonized by the English & presumably English cats. It raises the same question as the Japanese anomaly: are there large cross-national differences in catnip response rates, and if so, might they be genetic in origin, perhaps due to founder effects or genetic drift?
-
-
Australia: 12-2017-08-15, 200024ya responses $0.12$0.12017 = $243.55$2002017, Australia general population (raw responses); followup survey to confirm the 47% anomaly in the first Australian survey:
-
Have you ever given catnip to your cat? [n = 200123ya]
[randomized order]
-
No: I do not have a cat [n = 1438586ya / 71%]
-
No: I have a cat but have not tried catnip [n = 293 / 15%]
-
Yes: but they did not respond to catnip [n = 120 / 7.4%]
-
Yes: they responded to catnip [n = 150 / 6.5%]
120⁄270 = 44%. Pooled: 316⁄690 = 46%.
-
-
Australia: 2017-08-22–4d2017-08-25, 500 res$0.12$0.12017 = $60.89$502017, Australia general population (raw responses); adaptive sampling followup:
-
non-owner: 361 (74%)
-
non-trier: 75 (16%)
-
responder: 29 (5%)
-
non-responder: 25 (4.9%)
46% immunity rate, no surprise there.
-
-
Australia: 2017-08-29–4d2017-09-01, 150 res$0.12$0.12017 = $18.27$152017, Australia general population (raw responses); adaptive sampling followup:
-
Non-owner: n = 108 (75.1%)
-
Non-trier: n = 28 (15.7%)
-
Immune: n = 11 (7.4%)
-
Responder: n = 4 (1.8%)
-
-
UK: 2017-08-07–4d2017-08-10, 3000 res$0.12$0.12017 = $365.33$3002017, United Kingdom general population (raw responses)
-
Have you ever given catnip to your cat? [n = 3021]
[randomized order]
-
No: I do not have a cat [n = 2131 / 70%]
-
No: I have a cat but have not tried catnip [n = 265 / 9%]
-
Yes: but they did not respond to catnip [n = 162 / 5.5%]
-
Yes: they responded to catnip [n = 463 / 15.6%]
162⁄625 = 25.92% immunity rate.
-
-
USA: 2017-08-09–3d2017-08-11, 2700 responses $0.12$0.12017 = $328.79$2702017, USA general population (raw responses)
-
Have you ever given catnip to your cat?
[randomized order]
-
No: I do not have a cat [n = 1826198ya / 65%]
-
No: I have a cat but have not tried catnip [n = 269 / 9.6%]
-
Yes: but they did not respond to catnip [n = 151 / 5.1%]
-
Yes: they responded to catnip [n = 563 / 20.5%]
151⁄714 = 22% immunity rate. Pooling with previous 2 USA pilot surveys for a combined n = 3000:
-
No cat: n = 2027 / 68%
-
Cat but no tries: n = 300 / 10%
-
Cat and tried: n = 783 / 26%; result:
-
none/immune: n = 168 / 21%
-
responder: n = 615 / 79%
-
-
-
Mexico: 2017-08-11–3d2017-08-13, 3000 res$0.12$0.12017 = $365.33$3002017, Mexican general population (raw responses); Spanish version provided by David Figuera:
-
¿Alguna vez le ha dado nébeda (catnip/menta gatuna) a su gato? [n = 3011]
-
No: No tengo gato. [n = 2245 / 74.2%]
-
No: Tengo gato pero no lo he probado. [n = 594 / 19.8%]
-
Sí: Pero no le hizo efecto. [n = 82 / 3.3%]
-
Sí: Le hizo efecto. [n = 90 / 2.7%]
82⁄172 = 48% immunity rate. This is, like the first Australian sample, interestingly high but compromised by relatively small sample size: Mexicans apparently tend to own cats less and to be less likely to try catnip, so barely 5% of responses are useful.
-
-
Mexico: 2017-08-19–4d2017-08-22, 150 resraw responses); adaptive sampling followup:
-
Non-owner: 112 (75%)
-
Non-trier: 30 (20%)
-
Responder: 4 (2.5%)
-
Immune: 4 (2.2%)
4⁄8 = 50%.
-
-
Spain: 2017-08-11–4d2017-08-14, 3000 res$0.12$0.12017 = $365.33$3002017, Spanish general population (raw responses)
-
¿Alguna vez le ha dado nébeda (catnip/menta gatuna) a su gato? [n = 3000]
-
No: No tengo gato. [n = 2203 / 73.4%]
-
No: Tengo gato pero no lo he probado. [n = 607 / 21.2%]
-
Sí: Pero no le hizo efecto. [n = 87 / 2.4%]
-
Sí: Le hizo efecto. [n = 103 / 3%]
87⁄190 = 46% immunity rate. Similar to Mexico: low rates of cat ownership & catnip trying, high immunity rate.
-
-
Spain: 2017-08-19–4d2017-08-22 (raw responses); adaptive sampling followup:
-
Non-owner: 97 (68%)
-
Non-trier: 43 (24%)
-
Immune: 5 (4.7%)
-
Responder: 5 (3.7%)
5⁄10 = 50% immunity rate.
-
-
Germany: 2017-08-13–4d2017-08-16, 3000 res$0.12$0.12017 = $365.33$3002017, German general population (raw responses); German version provided by r0kit, checked by FeepingCreature & gehmehgeh1:
-
Haben Sie Ihrer Katze jemals Katzenminze/Catnip gegeben? [n = 3009]
-
Ich habe keine Katze. [n = 2093 / 71.3%]
-
Nein, bisher habe ich ihr keine Katzenminze/Catnip gegeben. [n = 536 / 16.4%]
-
Ja, aber sie reagiert nicht darauf. [n = 164 / 4.8%]
-
Ja, ich habe ihr Katzenminze/Catnip gegeben und sie reagiert darauf. [n = 216 / 7.4%]
164⁄380 = 43% immunity rate. Somewhat intermediate Spain & UK.
-
-
Japan: 2017-08-22–4d2017-08-25, 200 res$0.12$0.12017 = $24.36$202017, Japanese general population (raw responses); Japanese version provided by Juju Kurihara
-
自分のネコにキャットニップあげたことある? [n = 203]
[randomly reverse answer order; GS forbade full randomization]
-
いいえ。ネコは飼ってない。 [n = 162 / 84%]
-
いいえ。ネコはいるけど、キャットニップをあげたことない。 [n = 21 / 9%]
-
はい。でも反応がなかった。 [n = 6 / 1.9%]
-
はい。反応した。 [n = 14 / 4.7%]
6⁄20 = 30% immunity rate. Consistent with a low immunity rate but too small to rule out 10%/90%, requiring additional sampling.
-
-
Japan: 2017-08-25–4d2017-08-28, 3800 $0.12$0.12017 = $462.75$3802017, Japanese general population (raw responses); modified Japanese version with a catnip synonym for clarity, larger sample size:
-
自分のネコにキャットニップ(イヌハッカ)あげたことある? [n = 3828]
[randomly reverse answer order]
-
いいえ。ネコは飼ってない。 [n = 3158 / 83%]
-
いいえ。ネコはいるけど、キャットニップ(イヌハッカ)をあげたことない。 [n = 383 / 10.4%]
-
はい。でも反応がなかった。 [n = 82 / 2.4%]
-
はい。反応した。 [n = 205 / 4.5%]
82⁄287 = 29% immunity rate; pooling: 88⁄307 = 29%. This is an immunity rate similar to the UK and not otherwise remarkable, so the Japanese anomaly has been falsified.
-
-
Japan: 2017-08-29–3d2017-08-31, 150 $0.12$0.12017 = $18.27$152017, Japanese general population (raw responses); adaptive followup:
-
Non-owner: n = 127 (89.7%)
-
Non-trier: n = 11 (3.1%)
-
Immune: n = 4 (4.4%)
-
Responder: n = 9 (2.8%)
-
-
Brazil: 2017-08-25–3d2017-08-27, 3000 $0.12$0.12017 = $365.33$3002017, Brazilian general population (raw responses): Portuguese translation provided by Gladstone:
-
Você alguma vez deu erva-dos-gatos para seu gato? [n = 3045]
[randomized order]
-
Não: Não tenho gato. [n = 195173ya / 64%]
-
Não: Tenho gato, mas nunca tentei dar. [n = 781 / 26%]
-
Sim: Mas não fez efeito. [n = 139 / 4.5%]
-
Sim: E fez efeito. [n = 174 / 5.7%]
-
-
France & Portugal: omitted because I couldn’t find someone to check my French translation & ran out of money.
Adaptive Sampling
After completing my first pass over the available countries and while waiting on Japanese/French/Portuguese translations, I asked myself where should I spend my 4 $18.27$152017 GS coupons? This constitutes a classic adaptive sampling problem: choosing what datapoints to collect, based on previously collected data, in order to minimize a loss or maximize a reward, such as minimizing entropy or variance.
The Bayesian estimation of the binomial proportion’s parameter P follows the beta distribution based on successes/totals Β(α, β); one way to quantify the size of the posterior distribution over P is to estimate its entropy, which allows comparison of different posteriors and evaluation of what actions would reduce entropy the most:
bEntropy <- function(a,b) { lbeta(a, b) - (a-1) * digamma(a) - (b-1)*digamma(b) + (a+b-2)*digamma(a+b) }Estimating a binomial is influenced by the total sample size (bigger n means smaller posterior uncertainty) but also by the rate of successes (the closer to P = 0.5, the more informative about the proportion a given n is, while the closer to P = 0/1, the less we learn from each sample). So in the catnip surveys, Spain/Mexico samples yielded few samples (especially compared to USA/Canada) and are poorly estimated so we might want to collect more data there; but on the other hand, this small n is partially offset by the relatively high proportion P of immune responses which is easier to estimate; and on the gripping hand, each Spain/Mexico sample is 4× more expensive. It’s hard to say how it nets out.
We can ask by calculating the entropy reduction and relative cost of taking a hypothetical additional sample of n:
survey$Entropy <- unlist(Map(bEntropy, survey$Immune, survey$Triers))
n <- 50
survey$Entropy.hypothetical <- unlist(Map(function(a,b) { rate <- (a+1)/(b+1); bEntropy(a+(n*rate), n+b) },
survey$Immune, survey$Triers))
survey$Entropy.reduction <- survey$Entropy - survey$Entropy.hypothetical
survey$Entropy.cost <- survey$Entropy.reduction / survey$Cost
survey[order(survey$Entropy.cost),]
# Country Triers Immune Responders Cost Entropy Entropy.hypothetical Entropy.reduction Entropy.cost
# 3 Australia 759 352 407 0.74 −2.853405426 −2.885262214 0.03185678744 0.04304971276
# 8 Japan 320 92 228 1.29 −2.470193598 −2.542250267 0.07205666904 0.05585788297
# 5 Mexico 180 86 94 1.75 −2.135260348 −2.257230589 0.12197024173 0.06969728099
# 6 Spain 200 92 108 1.58 −2.188585162 −2.299631826 0.11104666446 0.07028269903
# 9 Brazil 313 139 174 0.96 −2.412869913 −2.486723486 0.07385357304 0.07693080525
# 4 Canada 842 147 695 0.37 −3.064821325 −3.093474193 0.02865286749 0.07744018239
# 7 Germany 380 164 216 0.79 −2.510847462 −2.572473801 0.06162633865 0.07800802360
# 2 UK 625 162 463 0.48 −2.822265042 −2.860566405 0.03830136288 0.07979450600
# 1 USA 783 168 615 0.38 −2.975320699 −3.006112449 0.03079175050 0.08103092236I repeated this calculation as new data arrived to decide where to sample next:
-
19 August: the next sample should come from Australia or Mexico. Due to a mistake in maximizing rather than minimizing, I began sampling from Canada/USA; deleting the USA survey did not seem to refund my coupon so I let Canada continue running and ran Mexico/Spain instead.
-
22 August: Australia
-
29 August: Australia, Japan
-
1 September: stopped sampling, but the entropy continues to recommend Australia/Japan/Mexico.
Results
Overall results as a table:
|
Country |
Start |
End |
Total |
Owners |
Non-owners |
Non-triers |
Triers |
Immune |
Responders |
Immunity rate |
$/response |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Canada |
2017-08-07 |
2017-08-22 |
3151 |
1114 |
2037 (65%) |
272 (9%) |
842 |
147 |
695 |
18% |
$0.45$0.372017 |
|
USA |
2017-07-28 |
2017-08-11 |
3110 |
1083 |
2027 (68%) |
300 (10%) |
783 |
168 |
615 |
21% |
$0.46$0.382017 |
|
UK |
2017-08-07 |
2017-08-10 |
3021 |
890 |
2131 (70%) |
265 (9%) |
625 |
162 |
463 |
26% |
$0.58$0.482017 |
|
Japan |
2017-08-22 |
2017-08-31 |
4182 |
735 |
3447 (82%) |
415 (10%) |
320 |
92 |
228 |
29% |
$1.57$1.292017 |
|
Germany |
2017-08-13 |
2017-08-16 |
3009 |
916 |
2093 (71%) |
536 (16%) |
380 |
164 |
216 |
43% |
$0.96$0.792017 |
|
Brazil |
2017-08-25 |
2017-08-28 |
3045 |
1094 |
1951 (64%) |
781 (26%) |
313 |
139 |
174 |
44% |
$1.17$0.962017 |
|
Spain |
2017-08-11 |
2017-08-22 |
3150 |
1601 |
2300 (73%) |
650 (21%) |
200 |
92 |
108 |
46% |
$1.92$1.582017 |
|
Australia |
2017-08-07 |
2017-09-01 |
5642 |
850 |
4041 (72%) |
842 (15%) |
759 |
356 |
403 |
47% |
$0.9$0.742017 |
|
Mexico |
2017-08-11 |
2017-08-22 |
3161 |
804 |
2357 (75%) |
624 (20%) |
180 |
86 |
94 |
48% |
$2.13$1.752017 |
|
31471 |
9087 |
22384 |
4685 |
4402 |
1406 |
2996 (68%) |
(32%) |
$0.86$0.712017 |
Meta-analyzing & plotting results:
survey <- read.csv(stdin(), header=TRUE, colClasses=c("factor", rep("integer", 6), "numeric", "numeric", "numeric"))
Country,Total,Owners,Non-owners,Non-triers,Triers,Immune,Responders,Immunity rate,Cost
Canada,3151,1114,2037,272,842,147,695,0.18,0.37
USA,3110,1083,2027,300,783,168,615,0.21,0.38
UK,3021,890,2131,265,625,162,463,0.26,0.48
Japan,4182,735,3447,415,320,92,228,0.29,1.29
Germany,3009,916,2093,536,380,164,216,0.43,0.79
Brazil,3045,1094,1951,781,313,139,174,0.44,0.96
Australia,5642,1601,4041,842,759,356,403,0.47,0.74
Spain,3150,850,2300,650,200,92,108,0.46,1.58
Mexico,3161,804,2357,624,180,86,94,0.48,1.75
library(metafor)
rer <- rma(xi=Responders, ni=Triers, measure="PR", slab=Country, data=survey); rer
# Random-Effects Model (k = 9; tau^2 estimator: REML)
#
# tau^2 (estimated amount of total heterogeneity): 0.0144 (SE = 0.0075)
# tau (square root of estimated tau^2 value): 0.1202
# I^2 (total heterogeneity / total variability): 97.17%
# H^2 (total variability / sampling variability): 35.37
#
# Test for Heterogeneity:
# Q(df = 8) = 314.4524, p-val < 0.0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.6447 0.0409 15.7536 <.0001 0.5645 0.7249
reo <- rma(xi=Owners, ni=Total, measure="PR", slab=Country, data=survey); reo
# Random-Effects Model (k = 9; tau^2 estimator: REML)
#
# tau^2 (estimated amount of total heterogeneity): 0.0033 (SE = 0.0017)
# tau (square root of estimated tau^2 value): 0.0578
# I^2 (total heterogeneity / total variability): 98.31%
# H^2 (total variability / sampling variability): 59.18
#
# Test for Heterogeneity:
# Q(df = 8) = 559.7712, p-val < 0.0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.2936 0.0195 15.0921 <.0001 0.2554 0.3317
ret <- rma(xi=Triers, ni=Owners, measure="PR", slab=Country, data=survey); ret
# Random-Effects Model (k = 9; tau^2 estimator: REML)
#
# tau^2 (estimated amount of total heterogeneity): 0.0440 (SE = 0.0221)
# tau (square root of estimated tau^2 value): 0.2097
# I^2 (total heterogeneity / total variability): 99.53%
# H^2 (total variability / sampling variability): 212.85
#
# Test for Heterogeneity:
# Q(df = 8) = 1798.3983, p-val < 0.0001
#
# Model Results:
#
# estimate se zval pval ci.lb ci.ub
# 0.4723 0.0701 6.7399 <.0001 0.3350 0.6097
forest(rer, order="obs")
forest(reo, order="obs")
forest(ret, order="obs")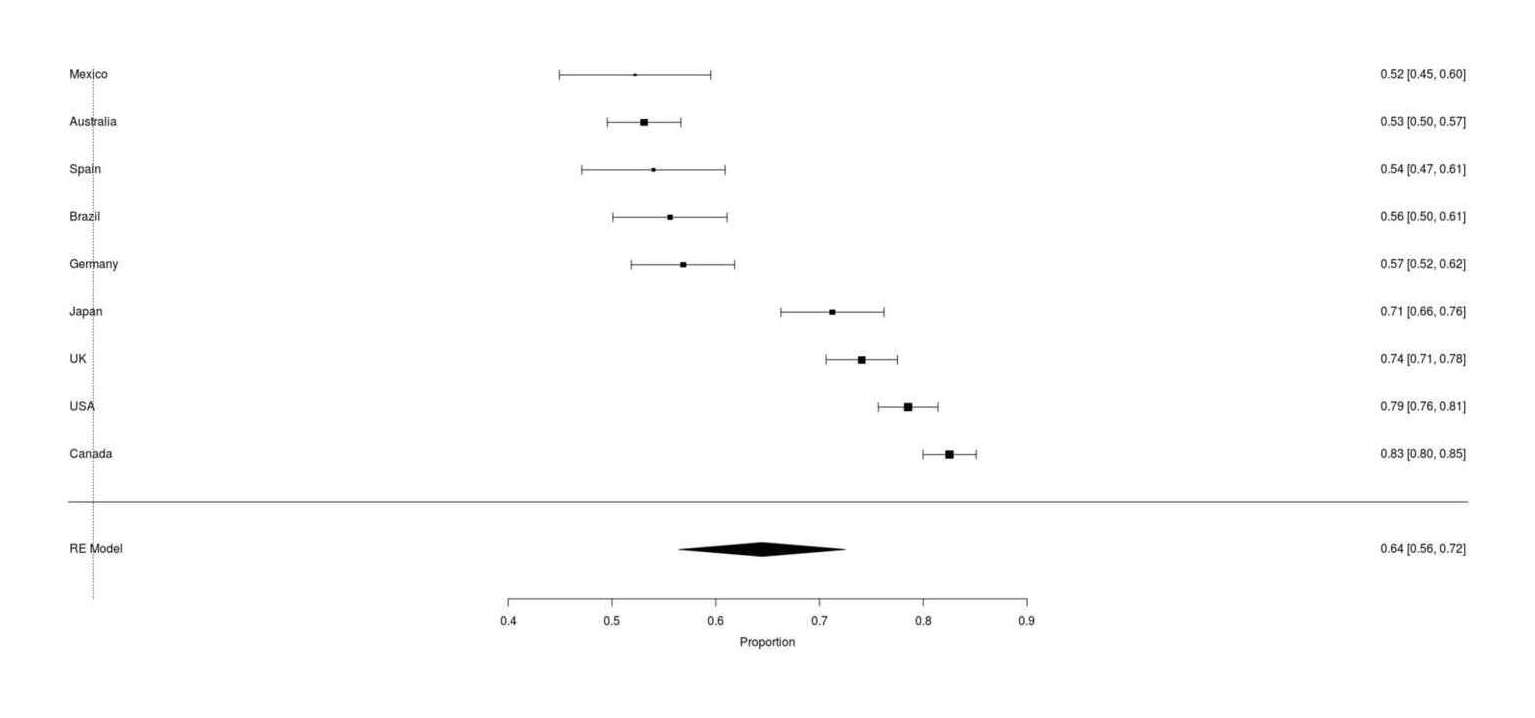
Full Google Survey results of ‘does your cat respond to catnip’ across 9 countries worldwide shows large differences in catnip immunity rates, from 17% to 48% of local cats reports to be immune.
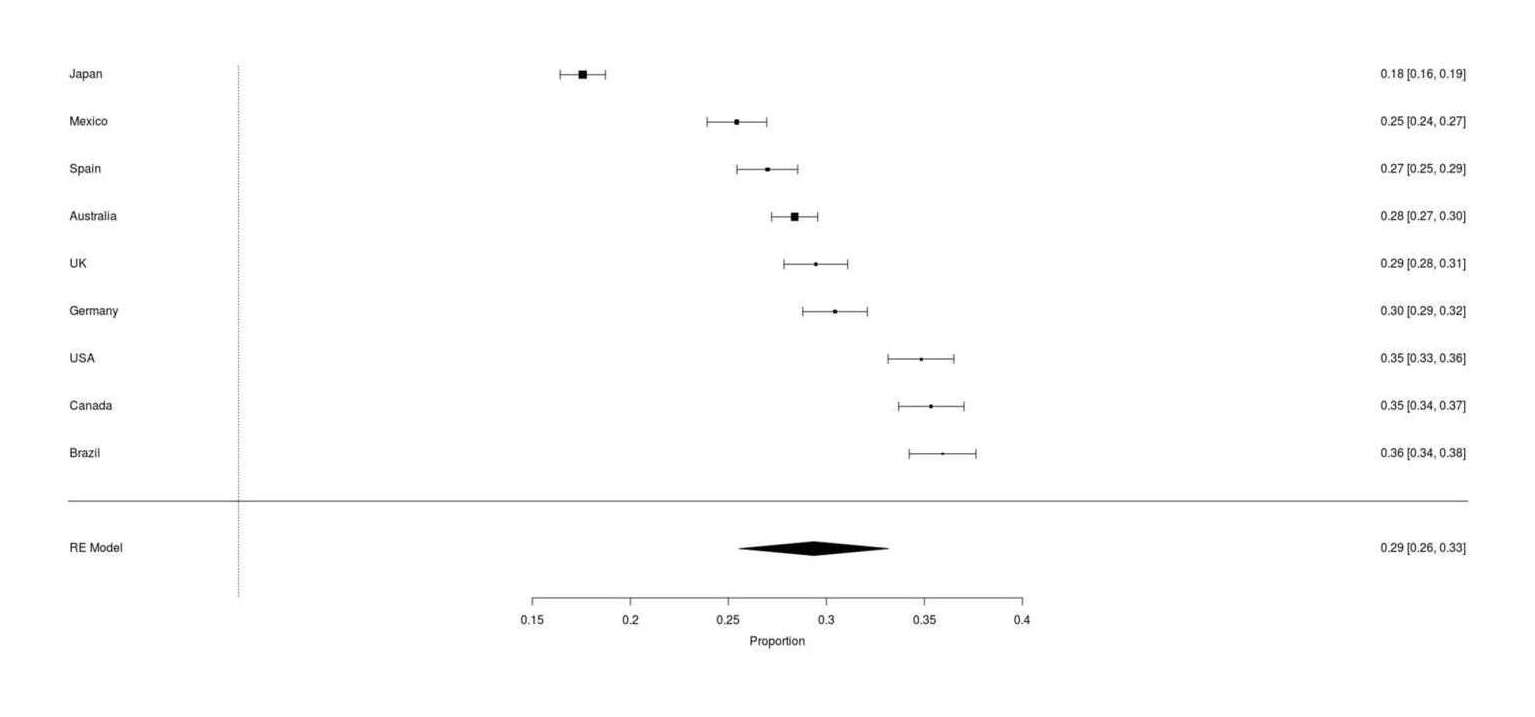
Google Survey results for whether respondents own a cat, across 9 countries (range: 17–35%, meta-analytic mean 29%)
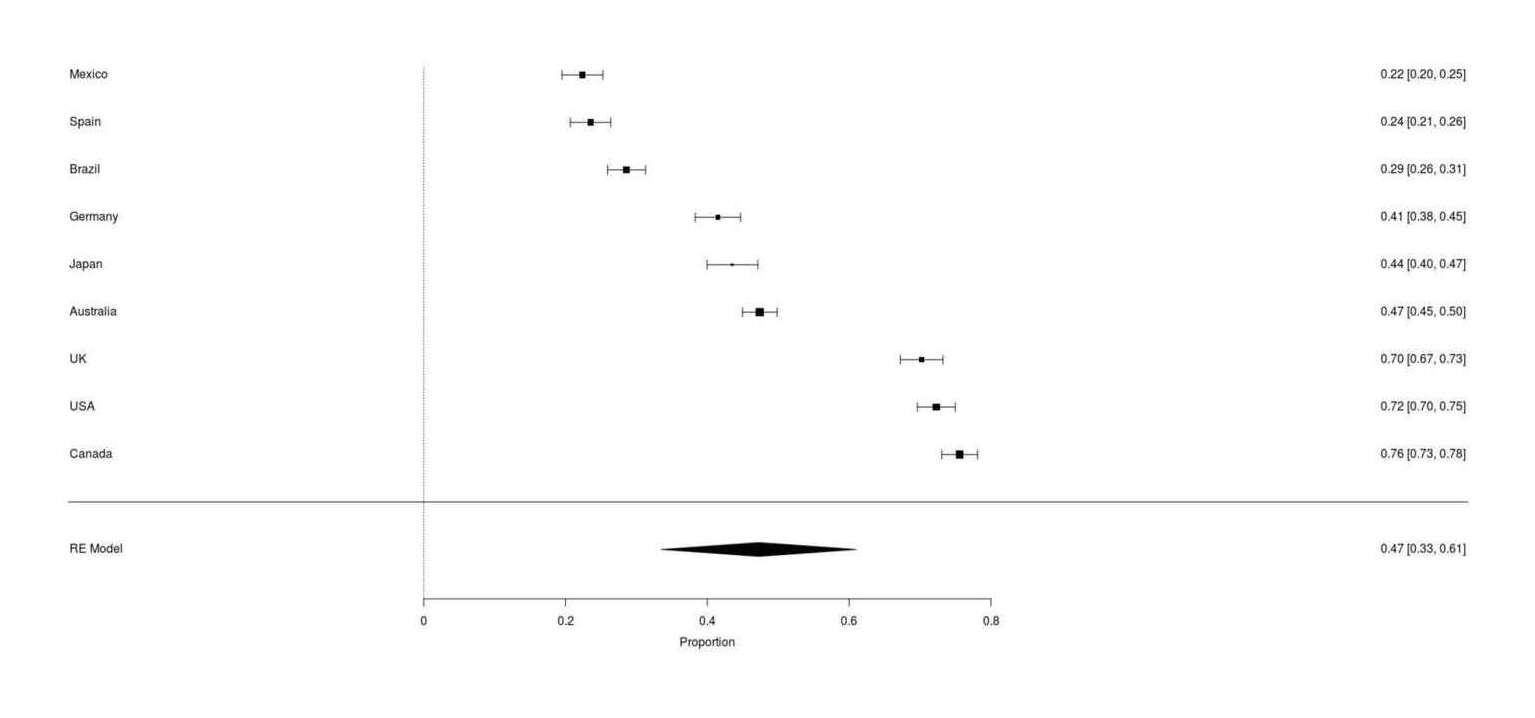
Google Survey results for whether respondents owning a cat have ever tried to use catnip, across 9 countries (range: 22–76%, meta-analytic mean 47%)
In the context of preliminary hypotheses from the catnip meta-analysis, there are 4 main conclusions offered by this large-n survey data (which increases the available sample size by >10×):
-
between-country differences exist
-
Japan does indeed have a high catnip response rate, but it is not extraordinarily high: Canadians report a higher catnip rate.
-
the overall average catnip response rate of 64% is almost identical to the prior meta-analytic result, suggesting that the survey is measuring the same thing as the research papers
-
further implying there is no temporal decline in catnip response rate, because then there would not be near-identity between 2017 results and the meta-analytic result
-
Intercorrelation
The extra data beyond the catnip response may itself be interesting. I noticed that beyond the expected differences in catnip response rate, the conditional probabilities of trying catnip given a cat, and having a cat given being surveyed, appeared to also differ considerably by country. That’s unexpected because you might think that whatever the number of cat owners, they will still use catnip at the same rate, and why would there be any correlation between proportion of cat owners and proportion of responding cats?
But the correlations and cross-country differences do seem to be there if I extract the estimated odds for each of the 3 transitions and correlate them:
library(brms)
bf_owner <- bf(Owners | trials(Total) ~ (1|Country))
bf_trier <- bf(Triers | trials(Owners) ~ (1|Country))
bf_response <- bf(Responders | trials(Triers) ~ (1|Country))
b2 <- brm(mvbf(bf_owner, bf_trier, bf_response, rescor=TRUE), data=survey, family=binomial()); summary(b2)
# Family: MV(binomial, binomial, binomial)
# Links: mu = logit
# mu = logit
# mu = logit
# Formula: Owners | trials(Total) ~ (1 | Country)
# Triers | trials(Owners) ~ (1 | Country)
# Responders | trials(Triers) ~ (1 | Country)
# Data: survey (Number of observations: 9)
# Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
# total post-warmup samples = 4000
#
# Group-Level Effects:
# ~Country (Number of levels: 9)
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sd(Owners_Intercept) 0.36 0.12 0.21 0.66 1279 1.00
# sd(Triers_Intercept) 1.10 0.35 0.65 1.99 1095 1.01
# sd(Responders_Intercept) 0.69 0.23 0.39 1.25 879 1.00
#
# Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Owners_Intercept −0.90 0.13 −1.15 −0.65 1200 1.00
# Triers_Intercept −0.12 0.39 −0.91 0.66 1397 1.00
# Responders_Intercept 0.64 0.24 0.14 1.12 1684 1.00
#
# Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
# is a crude measure of effective sample size, and Rhat is the potential
# scale reduction factor on split chains (at convergence, Rhat = 1).
ranef(b2)
# $Country
# , , Owners_Intercept
#
# Estimate Est.Error 2.5%ile 97.5%ile
# Australia −0.03044781685 0.1282204238 −0.284757218749 0.22717181030
# Brazil 0.31244611158 0.1292416296 0.054818130450 0.56888661855
# Canada 0.28798422855 0.1287040846 0.029973397220 0.54094918802
# Germany 0.06678857684 0.1316210852 −0.192722752913 0.32869035807
# Japan −0.64167774729 0.1296152408 −0.908276721935 −0.38242695654
# Mexico −0.17791601189 0.1310846382 −0.444852555408 0.07788323597
# Spain −0.09876368533 0.1298648872 −0.357686230169 0.16053092922
# UK 0.02140104376 0.1310367170 −0.242747351985 0.28399207800
# USA 0.26481992173 0.1299328820 0.001917056751 0.52942282197
#
# , , Triers_Intercept
#
# Estimate Est.Error 2.5%ile 97.5%ile
# Australia 0.01813788471 0.3885912273 −0.7845149100 0.8040397117941
# Brazil −0.78819571684 0.3897722924 −1.5862075480 0.0000443689147
# Canada 1.24883013037 0.3910430281 0.4505231495 2.0407819682118
# Germany −0.22112710148 0.3918324328 −1.0328674986 0.5774945667231
# Japan −0.13662809470 0.3923860668 −0.9279937053 0.6697218032907
# Mexico −1.11467805618 0.3925868958 −1.9009480273 −0.3266023072477
# Spain −1.05038700392 0.3941149256 −1.8671042045 −0.2640132172055
# UK 0.97769227307 0.3925479698 0.1787478323 1.7702763329297
# USA 1.07751793313 0.3914604603 0.2712072935 1.8478001989406
#
# , , Responders_Intercept
#
# Estimate Est.Error 2.5%ile 97.5%ile
# Australia −0.5044582315 0.2493370825 −1.00260681092 0.001552354279
# Brazil −0.3994089762 0.2626963885 −0.93710540902 0.129480329954
# Canada 0.8979007384 0.2520710317 0.41513927176 1.406509591116
# Germany −0.3499764734 0.2544537933 −0.83667455510 0.158186916451
# Japan 0.2625833744 0.2637053887 −0.25947489277 0.794264287381
# Mexico −0.5169044777 0.2728149763 −1.05988425248 0.016712965363
# Spain −0.4517022250 0.2690081731 −0.99083076217 0.059135851124
# UK 0.4037822551 0.2535945318 −0.09353189908 0.907456763495
# USA 0.6483597746 0.2498113059 0.15065734268 1.150894764620
predict(b2)
# , , Owners
#
# Estimate Est.Error 2.5%ile 97.5%ile
# [1,] 1111.27925 37.58129665 1040.975 1185
# [2,] 1080.40375 37.51611121 1007.975 1153
# [3,] 889.20850 34.94478233 822.000 957
# [4,] 740.43200 35.03746255 674.000 810
# [5,] 915.39250 36.13518205 844.000 988
# [6,] 1091.52625 36.50583488 1019.000 1162
# [7,] 1602.28800 47.89174209 1511.000 1698
# [8,] 851.73325 34.99259514 783.000 920
# [9,] 806.16650 34.95533216 736.000 874
#
# , , Triers
#
# Estimate Est.Error 2.5%ile 97.5%ile
# [1,] 840.94325 19.34487233 804 879.025
# [2,] 781.85675 20.74558566 740 822.000
# [3,] 624.06650 19.51606510 585 661.000
# [4,] 319.90550 19.20555344 282 357.000
# [5,] 380.15950 21.12151958 340 422.000
# [6,] 314.26450 21.08638657 274 355.025
# [7,] 758.91825 28.71753369 702 814.000
# [8,] 201.20300 17.40087609 168 235.000
# [9,] 180.57550 16.36839274 149 213.000
#
# , , Responders
#
# Estimate Est.Error 2.5%ile 97.5%ile
# [1,] 692.56225 15.156518563 661 721
# [2,] 613.27625 16.416586491 581 644
# [3,] 461.62275 15.665416808 431 491
# [4,] 227.27925 11.224427218 205 249
# [5,] 216.88525 13.221357098 191 243
# [6,] 174.94050 12.507720436 150 199
# [7,] 404.40200 19.807409709 365 444
# [8,] 109.10050 9.863428489 90 128
# [9,] 95.48250 9.350965399 77 113
owners <- ranef(b2)$Country[,,1][,1]
triers <- ranef(b2)$Country[,,2][,1]
responders <- ranef(b2)$Country[,,3][,1]
odds <- data.frame(Country=rownames(ranef(b2)$Country[,,3]), Owners=owners, Triers=triers, Responders=responders)
odds
# Owners Triers Responders
# Australia −0.03044781685 0.01813788471 −0.5044582315
# Brazil 0.31244611158 −0.78819571684 −0.3994089762
# Canada 0.28798422855 1.24883013037 0.8979007384
# Germany 0.06678857684 −0.22112710148 −0.3499764734
# Japan −0.64167774729 −0.13662809470 0.2625833744
# Mexico −0.17791601189 −1.11467805618 −0.5169044777
# Spain −0.09876368533 −1.05038700392 −0.4517022250
# UK 0.02140104376 0.97769227307 0.4037822551
# USA 0.26481992173 1.07751793313 0.6483597746
cor(odds)
# Owners Triers Responders
# Owners 1.0000000000
# Triers 0.3638358320 1.0000000000
# Responders 0.2072588658 0.8879400319 1.0000000000
library("GGally")
ggpairs(odds, columns=1:3, lower=list(mapping=aes(color=Country)))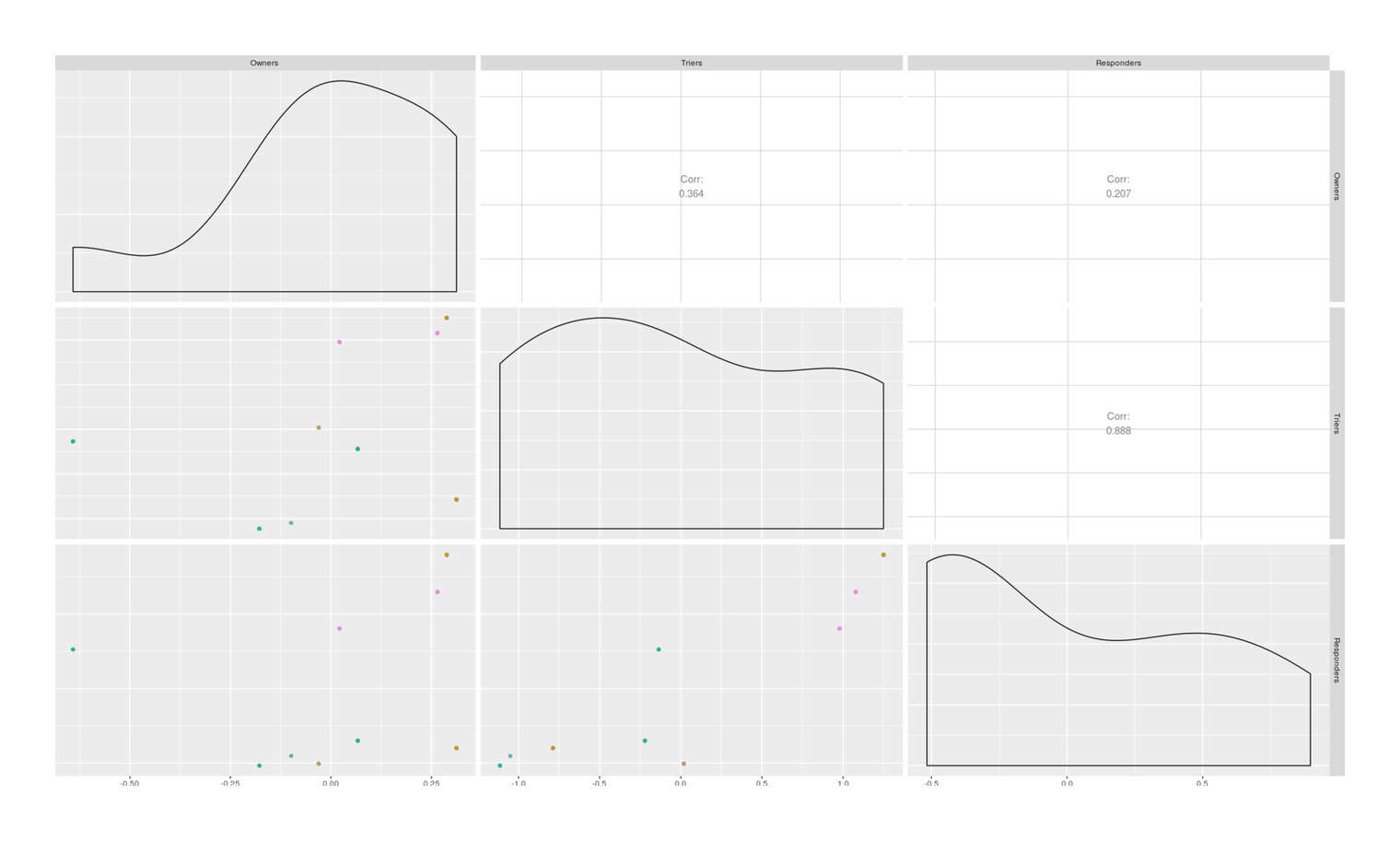
Scatterplot of log odds of cat ownership, catnip experimentation, and catnip response by country
Convenience Sampling: 2016 Google Docs Survey
In an attempt to get richer information about catnip response, including age/sex/gender/country, and investigate catnip alternatives like valerian & silvervine, I set up a Google Docs survey with incentives (Amazon gift card) and advertised online in various places I frequent or which are cat-related.
Questions
Standard demographics:
-
gender
-
age
-
country
Google Docs doesn’t make it easy to handle responses about potentially multiple cats an owner might have experimented with, so I hardwired it to a max of 5 cats with repeated blocks of questions. For each of 5 cats:
-
sex (M/F)
-
spayed/neutered
-
breed: various
-
fur color; used color list from “The Relationship Between Coat Color and Aggressive Behaviors in the Domestic Cat”, et al 2016:
-
black
-
black-and-white
-
calico
-
color points
-
gray
-
gray-and-white
-
Tabby (black, brown, and gray)
-
Tabby (orange, cream, and buff)
-
tortoiseshell
-
white
-
Torbie
-
other
-
personality 1–5: (“Catnip and the Cat Response”: “…The personality and emotional factors were found to be the most important: withdrawn cats react poorly while friendly, outgoing cats react best.”)
-
-
age at first administration
-
stimulants, binary: catnip response, valerian response, honeysuckle response, silvervine response, cat thyme
Human catnip use (common historically):
-
has the person ever consumed catnip in the form of: tea / leaves or a herb / roots / smoked / poultice
-
if so, what was the purpose? relaxation / stimulation / euphoria or intoxication / hallucination or visual distortion / dreams / insomnia / stomach aches / mosquito repellent / headaches / colds or flu or fever / hives / arthritis / increasing urination / treatment of worms / hemorrhoids / other
-
efficacy: 1–5
Launch
The survey was launched 2016-09-29, planned to run all year, incentivized with 3 $62.53$502016 Amazon gift cards, and advertised in the following places:
-
my Twitter
-
Google+
-
Gwern.net site header
Post-launch edits:
-
removed free response from gender question in demographic section due to abuse
-
added age constraints to the human and cat age questions due to abuse
-
edited introduction to rephrase it as “cat non-responses” & began advertising as a “catnip non-response” survey: the first 49 respondents claimed that 45 of 47 cats (cat #1 responses) responded to catnip, which is grossly discrepant from the 62% estimate - it’s imprecise, but there’s no way the true catnip rate is 96%! Further, the catnip non-response rate goes up in the additional cat entries. All this indicates either a bias in respondent recollections (they only remember the cats which do respond, or they provide a responding cat’s data first and then don’t include all the rest they know of) or a response bias to experimenter demand (inferring that I want to hear only about cats which do respond). The response rates for the other substances like silvervine are more reasonable thus far (although with far smaller sample sizes) and the small sample size is what I expected because those substances are much rarer, so this may not be a general acquiescence bias (because you would expect many more people to be claiming their cat respond to all of catnip/silvervine/valerian/thyme). If it’s a recollection bias, I don’t know of anyway to correct that afterwards or change the survey to eliminate it, so surveys on this topic might be futile.
-
final survey: Google Docs survey preview; mirror of final survey
The survey collected 241 responses from 2016-09-29 to 2017-01-02, when I closed it and awarded the gift cards. After filtering for quality, there were 223 responses.
Results
Cleaning
Google Surveys, as mentioned, doesn’t seem to support any elegant way of repeating a series of questions, so I hardcoded questions for up to 5 cats, producing a ‘wide’ survey format in which each row is a single respondent with 5 sets of age/breed/fur/neuter/sex/personality+catnip/valerian/silvervine/thyme/honeysuckle ratings. For almost all tasks, it’s better to have the survey in a ‘long’ format, where each row is instead a single cat’s set of covariates & ratings, with the owner information (and a unique ID) repeated across the rows for all the cats they provided information on. (This then permits straightforward analyses like regressions of the form Catnip ~ (1|ID) + Sex + Breed etc.) This is complicated enough I couldn’t figure out how to use the usual reshaping libraries to convert wide to long, so I did it by brute force. As well, an additional variable is added to investigate the demand bias, noting whether a cat entry is the “first” cat provided by a user; if there is a demand bias as I hypothesize based on the extremely high reported catnip response rates for first cats, then first vs the rest (second/third/fourth/fifth) should predict catnip responses.
After the data is reshaped, the free response fields need to be cleaned up and similar responses combined (eg. “UK” combined with “United Kingdom”).
catnip <- read.csv("https://gwern.net/doc/cat/psychology/drug/catnip/survey/2017-01-02-catnipsurvey-conveniencesample.csv")
catnip$ID <- 1:nrow(catnip); catnip$Timestamp <- NULL
catnipLong <- data.frame(ID=integer(), Owner.age=integer(), Owner.sex=factor(), Owner.education=factor(),
Owner.country=factor(), Catnip.types=factor(), Nth.cat=integer(), Cat.age=numeric(), Cat.breed=factor(),
Cat.fur.color=factor(), Cat.neuter=logical(), Cat.personality=integer(), Cat.sex=factor(),
Cat.response.Catnip=logical(), Cat.response.Valerian=logical(), Cat.response.Silvervine=logical(),
Cat.response.Thyme=logical(), Cat.response.Honeysuckle=logical())
for (i in 1:nrow(catnip)) {
catnipLong <- with(catnip[i,],
rbind(catnipLong,
data.frame(ID=ID, Owner.age=Owner.age, Owner.sex=Owner.sex, Owner.education=Owner.education, Owner.country=Owner.country, Catnip.types=Catnip.types,
Nth.cat=1, Cat.age=Cat1.age, Cat.breed=Cat1.breed, Cat.fur.color=Cat1.fur.color, Cat.neuter=Cat1.neuter, Cat.personality=Cat1.personality,
Cat.sex=Cat1.sex, Cat.response.Catnip=Cat1.response.Catnip, Cat.response.Valerian=Cat1.response.Valerian, Cat.response.Silvervine=Cat1.response.Silvervine,
Cat.response.Thyme=Cat1.response.Thyme, Cat.response.Honeysuckle=Cat1.response.Honeysuckle),
data.frame(ID=ID, Owner.age=Owner.age, Owner.sex=Owner.sex, Owner.education=Owner.education, Owner.country=Owner.country, Catnip.types=Catnip.types,
Nth.cat=2, Cat.age=Cat2.age, Cat.breed=Cat2.breed, Cat.fur.color=Cat2.fur.color, Cat.neuter=Cat2.neuter, Cat.personality=Cat2.personality,
Cat.sex=Cat2.sex, Cat.response.Catnip=Cat2.response.Catnip, Cat.response.Valerian=Cat2.response.Valerian,
Cat.response.Silvervine=Cat2.response.Silvervine, Cat.response.Thyme=Cat2.response.Thyme, Cat.response.Honeysuckle=Cat2.response.Honeysuckle),
data.frame(ID=ID, Owner.age=Owner.age, Owner.sex=Owner.sex, Owner.education=Owner.education, Owner.country=Owner.country, Catnip.types=Catnip.types,
Nth.cat=3, Cat.age=Cat3.age, Cat.breed=Cat3.breed, Cat.fur.color=Cat3.fur.color, Cat.neuter=Cat3.neuter, Cat.personality=Cat3.personality,
Cat.sex=Cat3.sex, Cat.response.Catnip=Cat3.response.Catnip, Cat.response.Valerian=Cat3.response.Valerian, Cat.response.Silvervine=Cat3.response.Silvervine,
Cat.response.Thyme=Cat3.response.Thyme, Cat.response.Honeysuckle=Cat3.response.Honeysuckle),
data.frame(ID=ID, Owner.age=Owner.age, Owner.sex=Owner.sex, Owner.education=Owner.education, Owner.country=Owner.country, Catnip.types=Catnip.types,
Nth.cat=4, Cat.age=Cat4.age, Cat.breed=Cat4.breed, Cat.fur.color=Cat4.fur.color, Cat.neuter=Cat4.neuter, Cat.personality=Cat4.personality, Cat.sex=Cat4.sex,
Cat.response.Catnip=Cat4.response.Catnip, Cat.response.Valerian=Cat4.response.Valerian, Cat.response.Silvervine=Cat4.response.Silvervine,
Cat.response.Thyme=Cat4.response.Thyme, Cat.response.Honeysuckle=Cat4.response.Honeysuckle),
data.frame(ID=ID, Owner.age=Owner.age, Owner.sex=Owner.sex, Owner.education=Owner.education, Owner.country=Owner.country, Catnip.types=Catnip.types,
Nth.cat=5, Cat.age=Cat5.age, Cat.breed=Cat5.breed, Cat.fur.color=Cat5.fur.color, Cat.neuter=Cat5.neuter, Cat.personality=Cat5.personality,
Cat.sex=Cat5.sex, Cat.response.Catnip=Cat5.response.Catnip, Cat.response.Valerian=Cat5.response.Valerian, Cat.response.Silvervine=Cat5.response.Silvervine,
Cat.response.Thyme=Cat5.response.Thyme, Cat.response.Honeysuckle=Cat5.response.Honeysuckle)))
}
## filter out the empty data-frame rows by filtering on `Cat.sex` - potential false positives, but anyone who doesn't even know the gender of their cat can't be a good judge of their responses anyway...
catnipLong <- catnipLong[!is.na(catnipLong$Cat.sex),]
## Test response bias:
catnipLong$First <- catnipLong$Nth.cat==1
catnipLong[!is.na(catnipLong$Cat.fur.color) &
catnipLong$Cat.fur.color=="Orange and white on left here http://b.robnugen.com/cats/kawasaki/cats_2015-03-26_09.22.26.jpg",]$Cat.fur.color <-
"Tabby (orange, cream, and buff)"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="Orange and white splotched",]$Cat.fur.color <- "Tabby (orange, cream, and buff)"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="tortoiseshell",]$Cat.fur.color <- "Torbie (tortoiseshell colors with tabby pattern)"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="white",]$Cat.fur.color <- "gray-and-white"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="Orange tabby with paint/large white areas",]$Cat.fur.color <- "Tabby (orange, cream, and buff)"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="Tabby/Tuxedo pattern mix (black and white)",]$Cat.fur.color <- "black-and-white"
catnipLong[!is.na(catnipLong$Cat.fur.color) & catnipLong$Cat.fur.color=="tuxedo black & white longhair",]$Cat.fur.color <- "black-and-white"
levels(catnipLong$Cat.fur.color) <- c(levels(catnipLong$Cat.fur.color), "Other")
usableFurColors <- row.names(sort(table(catnipLong$Cat.fur.color)))[22:29]
catnipLong[!is.na(catnipLong$Cat.fur.color) & !(catnipLong$Cat.fur.color %in% usableFurColors),]$Cat.fur.color <- "Other"
## use only breeds with n>3, lump the rest together:
usableBreeds <- row.names(sort(table(catnipLong$Cat.breed))[26:30])
levels(catnipLong$Cat.breed) <- c(levels(catnipLong$Cat.breed), "Other")
catnipLong[!is.na(catnipLong$Cat.breed) & !(catnipLong$Cat.breed %in% usableBreeds),]$Cat.breed <- "Other"
## Clean up country free responses:
replaceFactor <- function(df, wrong,right) { df[!is.na(df$Owner.country) & df$Owner.country==wrong,]$Owner.country <- right
return(df) }
catnipLong <- replaceFactor(catnipLong, "Czech republic", "Czech Republic")
catnipLong <- replaceFactor(catnipLong, "Czech Republic ", "Czech Republic")
catnipLong <- replaceFactor(catnipLong, "india", "India")
catnipLong <- replaceFactor(catnipLong, "latvia", "Latvia")
catnipLong <- replaceFactor(catnipLong, "N/A", NA)
catnipLong <- replaceFactor(catnipLong, "Sweden ", "Sweden")
catnipLong <- replaceFactor(catnipLong, "UK", "United Kingdom")
write.csv(catnipLong, file="catnip-long-clean.csv", row.names=FALSE)Descriptive
Roughly 391 cat entries survive cleaning. In general, the data suffers from high levels of missingness on the owner/cat covariates, and unfortunately, there are very few responses dealing with non-catnip (I had hoped more cat owners would’ve tried them but apparently not):
-
Catnip: n = 352
-
Honeysuckle: 43
-
Silvervine: 16
-
Thyme: 31
-
Valerian: 47
catnip <- read.csv("https://gwern.net/doc/cat/psychology/drug/catnip/survey/2017-01-02-catnipsurvey-conveniencesample-long-clean.csv")
library(skimr)
skim(catnip)
# Skim summary statistics
# n obs: 391
# n variables: 19
# Note: no visible binding for global variable 'self'
#
# Variable type: factor
# variable missing complete n n_unique top_counts ordered
# Cat.breed 31 360 391 6 dom: 263, dom: 44, Oth: 34, NA: 31 FALSE
# Cat.fur.color 29 362 391 9 Oth: 100, bla: 60, bla: 53, Tab: 44 FALSE
# Catnip.types 5 386 391 17 dry: 201, dry: 49, dry: 44, fre: 20 FALSE
# Cat.sex 0 391 391 2 mal: 201, fem: 190, NA: 0 FALSE
# Owner.country 1 390 391 24 USA: 247, Uni: 40, Can: 39, Fra: 7 FALSE
# Owner.education 17 374 391 6 bac: 156, hig: 79, ass: 46, mas: 44 FALSE
# Owner.sex 19 372 391 3 mal: 254, fem: 113, NA: 19, oth: 5 FALSE
#
# Variable type: integer
# variable missing complete n mean sd p0 p25 p50 p75 p100 hist
# Cat.personality 29 362 391 3.58 1.21 1 3 4 5 5 ▂▅▁▅▁▇▁▇
# ID 0 391 391 111.92 64.56 1 56.5 113 168.5 223 ▇▆▇▇▇▆▇▇
# Nth.cat 0 391 391 1.59 0.8 1 1 1 2 5 ▇▅▁▁▁▁▁▁
# Owner.age 36 355 391 28.8 8.93 14 23 28 32 85 ▃▇▃▁▁▁▁▁
#
# Variable type: logical
# variable missing complete n mean count
# Cat.neuter 25 366 391 0.94 TRU: 345, NA: 25, FAL: 21
# Cat.response.Catnip 39 352 391 0.85 TRU: 300, FAL: 52, NA: 39
# Cat.response.Honeysuckle 348 43 391 0.4 NA: 348, FAL: 26, TRU: 17
# Cat.response.Silvervine 375 16 391 0.25 NA: 375, FAL: 12, TRU: 4
# Cat.response.Thyme 360 31 391 0.39 NA: 360, FAL: 19, TRU: 12
# Cat.response.Valerian 344 47 391 0.66 NA: 344, TRU: 31, FAL: 16
# First 0 391 391 0.57 TRU: 222, FAL: 169, NA: 0
#
# Variable type: numeric
# variable missing complete n mean sd p0 p25 p50 p75 p100 hist
# Cat.age 59 332 391 2.15 2.23 0 1 1 3 18 ▇▂▁▁▁▁▁▁
## Visualize missingness:
library(visdat)
catnipMissing <- catnip
catnipMissing$Cat.sex <- catnipMissing$ID <- catnipMissing$Nth.cat <- catnipMissing$First <- NULL
vis_miss(catnipMissing)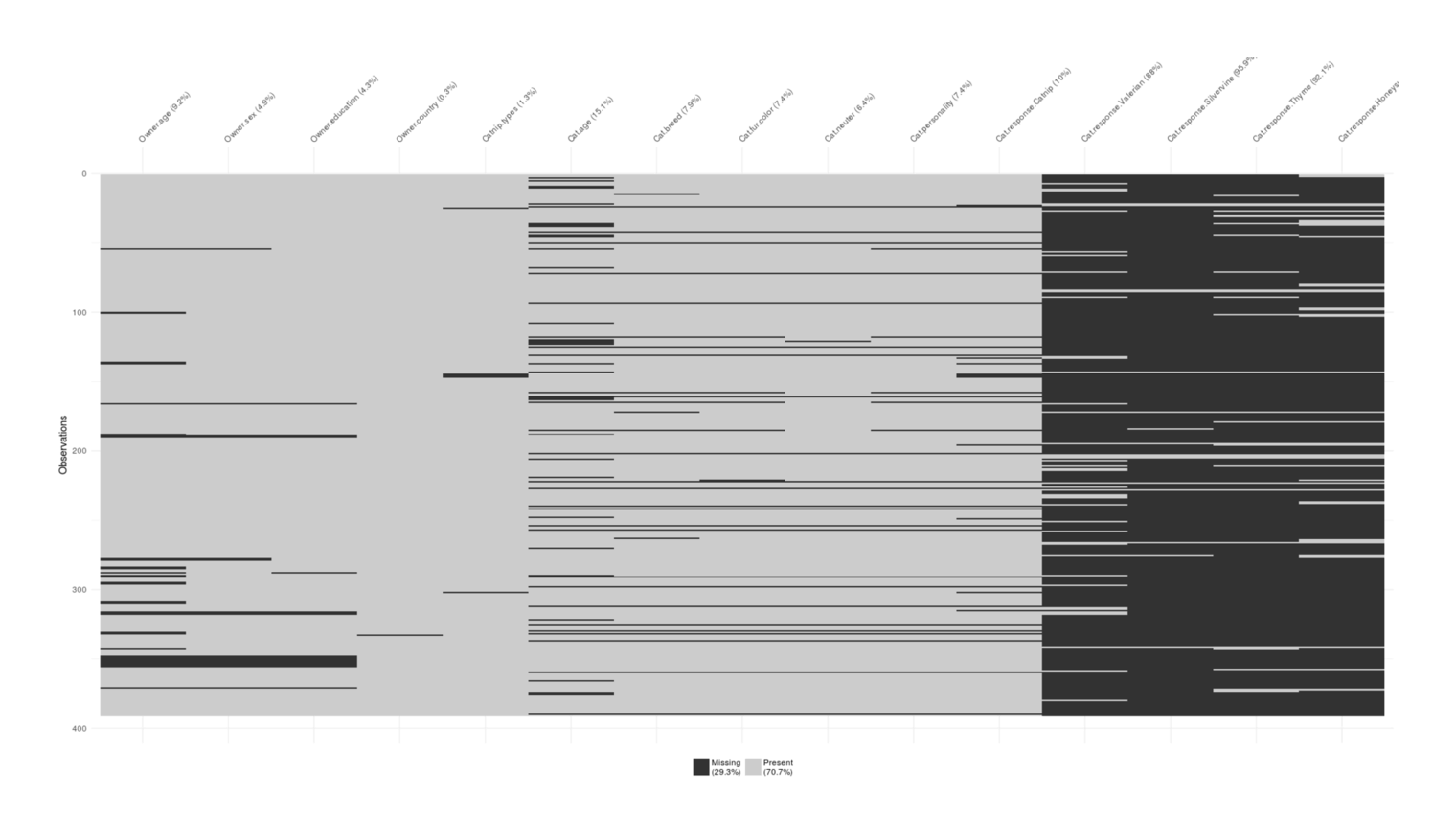
Visualizing degree of missingness in the convenience sample survey: primarily concentrated in the non-catnip response questions.
Presenting the catnip raw data in more detail (split by the covariates from the meta-analysis):
s <- aggregate(Cat.response.Catnip ~ Owner.country + Cat.age + Cat.breed + Cat.sex,
function(x){c(sum(x), length(x), round(digits=2,mean(x)))}, data=catnip)
s[order(s$Owner.country, s$Cat.age, s$Cat.breed),]|
Owner country |
Cat age |
Cat breed |
Cat sex |
Responders |
N |
Percentage |
|---|---|---|---|---|---|---|
|
Australia |
1.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
Australia |
1.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Australia |
2.00 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
Australia |
6.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Belarus |
3.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
Canada |
0.50 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
Canada |
0.50 |
domestic short-haired (mixed) |
male |
0 |
1 |
0.00 |
|
Canada |
0.50 |
Other |
male |
1 |
1 |
1.00 |
|
Canada |
1.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Canada |
1.00 |
domestic short-haired (mixed) |
male |
3 |
3 |
1.00 |
|
Canada |
1.00 |
Maine coon |
male |
1 |
1 |
1.00 |
|
Canada |
2.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Canada |
2.00 |
domestic short-haired (mixed) |
male |
2 |
3 |
0.67 |
|
Canada |
3.00 |
domestic short-haired (mixed) |
female |
2 |
3 |
0.67 |
|
Canada |
3.00 |
domestic short-haired (mixed) |
male |
2 |
3 |
0.67 |
|
Canada |
4.00 |
domestic short-haired (mixed) |
female |
2 |
2 |
1.00 |
|
Canada |
5.00 |
Other |
male |
1 |
1 |
1.00 |
|
Canada |
6.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Canada |
6.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Canada |
7.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Canada |
7.00 |
domestic short-haired (mixed) |
male |
1 |
2 |
0.50 |
|
Czech Republic |
1.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Czech Republic |
2.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Finland |
3.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Finland |
5.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
France |
0.00 |
domestic short-haired (mixed) |
female |
2 |
2 |
1.00 |
|
France |
3.00 |
Other |
male |
1 |
1 |
1.00 |
|
Germany |
0.60 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Germany |
1.00 |
domestic long-haired (mixed) |
male |
0 |
1 0 |
.00 |
|
Germany |
1.00 |
Other |
male |
0 |
1 |
0.00 |
|
Germany |
4.00 |
Other |
female |
0 |
1 0 |
.00 |
|
Germany |
6.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
India |
0.66 |
domestic long-haired (mixed) |
female |
1 |
1 1 |
.00 |
|
India |
1.00 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
India |
1.50 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
India |
2.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Ireland |
0.00 |
Other |
female |
1 |
1 1 |
.00 |
|
Italy |
1.00 |
domestic long-haired (mixed) |
male |
0 |
2 0 |
.00 |
|
Italy |
1.00 |
domestic short-haired (mixed) |
female |
2 |
2 |
1.00 |
|
Japan |
2.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Japan |
2.00 |
Other |
male |
1 |
1 |
1.00 |
|
Latvia |
1.00 |
domestic short-haired (mixed) |
female |
2 |
2 |
1.00 |
|
Latvia |
1.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Latvia |
5.00 |
Other |
male |
1 |
1 |
1.00 |
|
Netherlands |
0.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
Netherlands |
0.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
New Zealand |
0.50 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
New Zealand |
2.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Panama |
18.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Russia |
2.00 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
Slovenia |
1.00 |
domestic short-haired (mixed) |
female |
0 |
1 |
0.00 |
|
Slovenia |
2.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Slovenia |
4.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Spain |
0.00 |
Maine coon |
female |
0 |
1 0 |
.00 |
|
Spain |
0.00 |
Other |
male |
1 |
1 |
1.00 |
|
Sweden |
0.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
Sweden |
0.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
Sweden |
1.00 |
Maine coon |
male |
1 |
1 |
1.00 |
|
Sweden |
2.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
United Kingdom |
0.50 |
domestic long-haired (mixed) |
female |
1 |
1 1 |
.00 |
|
United Kingdom |
0.50 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
United Kingdom |
0.50 |
domestic short-haired (mixed) |
male |
0 |
1 |
0.00 |
|
United Kingdom |
1.00 |
domestic long-haired (mixed) |
female |
0 |
1 0 |
.00 |
|
United Kingdom |
1.00 |
domestic short-haired (mixed) |
female |
5 |
5 |
1.00 |
|
United Kingdom |
1.00 |
domestic short-haired (mixed) |
male |
5 |
5 |
1.00 |
|
United Kingdom |
2.00 |
domestic long-haired (mixed) |
male |
0 |
1 0 |
.00 |
|
United Kingdom |
2.00 |
domestic short-haired (mixed) |
female |
1 |
2 |
0.50 |
|
United Kingdom |
2.00 |
domestic short-haired (mixed) |
male |
3 |
4 |
0.75 |
|
United Kingdom |
3.00 |
domestic short-haired (mixed) |
male |
3 |
3 |
1.00 |
|
United Kingdom |
3.00 |
Other |
male |
1 |
1 |
1.00 |
|
United Kingdom |
4.00 |
domestic short-haired (mixed) |
male |
1 |
2 |
0.50 |
|
United Kingdom |
4.00 |
Other |
male |
2 |
2 |
1.00 |
|
United Kingdom |
5.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
United Kingdom |
5.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
United Kingdom |
6.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
0.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
USA |
0.00 |
domestic short-haired (mixed) |
female |
3 |
3 |
1.00 |
|
USA |
0.00 |
domestic short-haired (mixed) |
male |
2 |
2 |
1.00 |
|
USA |
0.10 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
USA |
0.10 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
0.10 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
0.40 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
0.40 |
Maine coon |
male |
1 |
1 |
1.00 |
|
USA |
0.50 |
domestic short-haired (mixed) |
female |
3 |
5 |
0.60 |
|
USA |
0.50 |
domestic short-haired (mixed) |
male |
7 |
7 |
1.00 |
|
USA |
0.50 |
Other |
male |
1 |
1 |
1.00 |
|
USA |
0.75 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
0.75 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
0.80 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
USA |
0.80 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
1.00 |
domestic long-haired (mixed) |
female |
6 |
8 0 |
.75 |
|
USA |
1.00 |
domestic long-haired (mixed) |
male |
4 |
4 1 |
.00 |
|
USA |
1.00 |
domestic short-haired (mixed) |
female |
29 |
33 |
0.88 |
|
USA |
1.00 |
domestic short-haired (mixed) |
male |
27 |
33 |
0.82 |
|
USA |
1.00 |
Maine coon |
male |
3 |
3 |
1.00 |
|
USA |
1.00 |
Other |
female |
4 |
4 1 |
.00 |
|
USA |
1.00 |
Other |
male |
2 |
3 |
0.67 |
|
USA |
1.00 |
Russian Blue |
female |
0 |
1 0 |
.00 |
|
USA |
1.00 |
Russian Blue |
male |
2 |
2 |
1.00 |
|
USA |
2.00 |
domestic long-haired (mixed) |
female |
4 |
4 1 |
.00 |
|
USA |
2.00 |
domestic long-haired (mixed) |
male |
1 |
2 0 |
.50 |
|
USA |
2.00 |
domestic short-haired (mixed) |
female |
14 |
14 |
1.00 |
|
USA |
2.00 |
domestic short-haired (mixed) |
male |
12 |
15 |
0.80 |
|
USA |
2.00 |
Maine coon |
male |
2 |
2 |
1.00 |
|
USA |
2.00 |
Other |
female |
3 |
4 0 |
.75 |
|
USA |
2.00 |
Other |
male |
3 |
3 |
1.00 |
|
USA |
3.00 |
domestic long-haired (mixed) |
female |
1 |
2 0 |
.50 |
|
USA |
3.00 |
domestic long-haired (mixed) |
male |
3 |
3 1 |
.00 |
|
USA |
3.00 |
domestic short-haired (mixed) |
female |
9 |
12 |
0.75 |
|
USA |
3.00 |
domestic short-haired (mixed) |
male |
10 |
10 |
1.00 |
|
USA |
3.00 |
Other |
female |
1 |
1 1 |
.00 |
|
USA |
3.00 |
Ragdoll |
male |
1 |
1 |
1.00 |
|
USA |
4.00 |
domestic short-haired (mixed) |
female |
4 |
4 |
1.00 |
|
USA |
4.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
4.00 |
Ragdoll |
female |
1 |
1 1 |
.00 |
|
USA |
4.00 |
Russian Blue |
female |
1 |
1 1 |
.00 |
|
USA |
5.00 |
domestic short-haired (mixed) |
female |
2 |
3 |
0.67 |
|
USA |
5.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
5.00 |
Other |
female |
0 |
1 0 |
.00 |
|
USA |
6.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
USA |
6.00 |
domestic short-haired (mixed) |
female |
2 |
2 |
1.00 |
|
USA |
6.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
7.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
8.00 |
domestic long-haired (mixed) |
male |
1 |
1 1 |
.00 |
|
USA |
9.00 |
domestic short-haired (mixed) |
male |
1 |
1 |
1.00 |
|
USA |
12.00 |
domestic short-haired (mixed) |
female |
1 |
1 |
1.00 |
|
USA |
17.00 |
Maine coon |
male |
1 |
1 |
1.00 |
|
Vietnam |
4.00 |
Other |
male |
0 |
1 |
0.00 |
Analysis
The primary questions here are:
-
what is the rate of catnip response by country?
-
is there a demand bias? If so, what is #1 adjusted for that?
-
do any of the covariates predict catnip response? In descending order of plausibility: age, breed, sex, neuter status, fur color, and owner sex/education/age.
-
how does the catnip response correlate with responses to the alternatives like silvervine? Can responses to one be used to predict the others, giving insight into the biological mechanisms or guide owners in selection?
-
what do humans think of catnip as a herbal remedy?
Catnip Response Rates
Since the other drugs are too rare to be worth analyzing, I focus on the catnip responses.
I set up a Bayesian multilevel logistic regression model in brms/Stan to investigate. Notes on model details:
-
each row is a single cat’s response, true/false, so it uses the binomial family (Bernoulli to be more specific, which is faster in Stan apparently) & is a logistic regression
-
non-catnip responses are excluded due to missingness (although one could try to use
brm_multiple’s support for data imputation, I ran into problems installing MICE) -
country & ID are treated as random effects to nest ratings in
-
most of the covariates are categorical/logical, but the 2 age variables are continuous; in many datasets, age is a nonlinear variable, and treated as a quadratic or higher polynomial, but
brmssupports splines so the human/cat age variables are given splines in case of any nonlinearity. Nonlinearity is also plausible here because catnip response only emerges at a particular age and the speculation about being related to feline sexual functions would also suggest possible trends like a quadratic. -
strong informative priors are used to keep estimates in ranges we know to be true and make the model stabler/faster:
-
a horseshoe prior is put on most of the covariates: the horseshoe is like the lasso in inducing sparsity, as is appropriate in this case because the categorical variables have many levels, and I a priori expect that most of the covariates are irrelevant (except for country and first-rating). Conveniently
brms’s horseshoe allows specifying expected fraction of nonzero coefficients, which I set at 20% (which is being generous). -
a normal prior of 𝒩(0,0.3) is put on the country-level random effects. The parameterization of the logistic model uses log-odds/logits, so the probabilities must be transformed. 0.3 here roughly reflects the observed distribution of country-level probabilities in the current meta-analysis, from 40–80%, which is 1 logit, and divided by 3, gives ~0.3. This will provide reasonable per-country results, especially in countries for which few respondents are available (most of them, given the skew to the USA).
-
another normal of 𝒩(0.66,0.1) is put on the overall intercept/base-rate of catnip response rate. The meta-analysis gives a global probability of catnip response of ~0.66, the logit of which is also 0.66. As the meta-analysis is fairly large, it is highly unlikely it’s off by too much, so it gets a narrower SD.
-
finally, a stronger prior is put on the spline degrees: if there is nonlinearity, it should be of quite low degree, not much more than quadratic - more is implausible and cannot be estimated from this dataset anyway
-
library(brms)
c <- brm(Cat.response.Catnip ~ (1|ID) + (1|Owner.country) + # random effects
s(Cat.age) + s(Owner.age) + # splines for possible nonlinearities
First + Owner.education + Owner.sex + Cat.neuter + Cat.breed + Cat.fur.color + Cat.sex, # covariates
# informative priors:
prior=c(set_prior("horseshoe(1, par_ratio=0.2)"), prior(student_t(3,0,1), class="sds"), prior(normal(0,0.3), class="sd"),
prior(normal(0.66,0.1), class="Intercept")),
family=bernoulli(), iter=20000, control=list(adapt_delta=0.90), data=catnip); summary(c)
# ... Data: catnip (Number of observations: 288)
# Samples: 4 chains, each with iter = 20000; warmup = 10000; thin = 1;
# total post-warmup samples = 40000
#
# Smooth Terms:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sds(sCat.age_1) 0.88 0.82 0.03 2.98 40000 1.00
# sds(sOwner.age_1) 0.76 0.63 0.03 2.33 29984 1.00
#
# Group-Level Effects:
# ~ID (Number of levels: 184)
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sd(Intercept) 0.22 0.17 0.01 0.62 22873 1.00
#
# ~Owner.country (Number of levels: 22)
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sd(Intercept) 0.62 0.16 0.35 0.96 40000 1.00
#
# Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Intercept 0.66 0.25 0.03 1.02 26509 1.00
# FirstTRUE 0.09 0.23 −0.04 0.84 19389 1.00
# Owner.educationbachelors 0.03 0.11 −0.07 0.38 30613 1.00
# Owner.educationhighschool −0.02 0.10 −0.26 0.09 33568 1.00
# Owner.educationmasters −0.01 0.09 −0.18 0.12 40000 1.00
# Owner.educationPhD 0.00 0.10 −0.14 0.18 40000 1.00
# Owner.educationprofessionaldegreeMDDJDDetc −0.02 0.12 −0.29 0.11 36396 1.00
# Owner.sexmale 0.00 0.07 −0.11 0.16 40000 1.00
# Owner.sexother 0.01 0.19 −0.16 0.23 40000 1.00
# Cat.neuterTRUE −0.02 0.14 −0.28 0.12 23840 1.00
# Cat.breeddomesticshortMhairedmixed 0.01 0.09 −0.09 0.25 40000 1.00
# Cat.breedMainecoon 0.01 0.13 −0.15 0.21 40000 1.00
# Cat.breedOther −0.00 0.09 −0.15 0.14 12387 1.00
# Cat.breedRagdoll 0.01 0.19 −0.18 0.22 35306 1.00
# Cat.breedRussianBlue −0.01 0.16 −0.26 0.14 18718 1.00
# Cat.fur.colorblackMandMwhite 0.07 0.25 −0.07 0.92 20627 1.00
# Cat.fur.colorcalico −0.04 0.21 −0.67 0.09 24589 1.00
# Cat.fur.colorcolorpointsdarkextremitylighterbody 0.00 0.12 −0.17 0.17 40000 1.00
# Cat.fur.colorgray −0.01 0.11 −0.23 0.12 36522 1.00
# Cat.fur.colorgrayMandMwhite −0.03 0.14 −0.39 0.09 29663 1.00
# Cat.fur.colorOther 0.04 0.15 −0.07 0.50 24049 1.00
# Cat.fur.colorTabbyorangecreamandbuff −0.00 0.08 −0.15 0.15 40000 1.00
# Cat.fur.colorTorbietortoiseshellcolorswithtabbypattern −0.02 0.12 −0.30 0.10 34896 1.00
# Cat.sexmale 0.01 0.08 −0.08 0.20 40000 1.00
# sCat.age_1 0.01 0.07 −0.06 0.21 34748 1.00
# sOwner.age_1 −0.01 0.07 −0.19 0.08 14852 1.00
## Grand mean/intercept converted to probability:
library(boot)
inv.logit(0.66)
# [1] 0.6592603885
## Country-level random-effects:
re <- ranef(c)$Owner.country
round(digits=2, inv.logit(re))
# , , Intercept
#
# Estimate Est.Error 2.5%ile 97.5%ile
# Australia 0.58 0.64 0.31 0.83
# Belarus 0.53 0.65 0.25 0.80
# Canada 0.59 0.60 0.41 0.77
# Czech Republic 0.55 0.64 0.29 0.81
# Finland 0.56 0.65 0.29 0.82
# France 0.58 0.64 0.32 0.83
# Germany 0.37 0.65 0.14 0.64
# India 0.45 0.63 0.21 0.71
# Ireland 0.53 0.65 0.26 0.80
# Italy 0.45 0.63 0.21 0.70
# Japan 0.57 0.65 0.30 0.83
# Latvia 0.53 0.65 0.25 0.80
# Netherlands 0.56 0.65 0.29 0.82
# New Zealand 0.55 0.65 0.28 0.81
# Panama 0.53 0.65 0.25 0.80
# Russia 0.44 0.65 0.18 0.72
# Slovenia 0.50 0.64 0.24 0.76
# Spain 0.47 0.64 0.21 0.74
# Sweden 0.60 0.64 0.34 0.84
# United Kingdom 0.62 0.59 0.44 0.78
# USA 0.77 0.56 0.68 0.85
# Vietnam 0.44 0.65 0.17 0.72
## Posterior for a generic set of covariates, by country:
round(digits=2, inv.logit(fitted(c, data.frame(Cat.response.Catnip=NA, ID=3, Owner.country=row.names(re), First=FALSE,
Owner.education="masters", Owner.age=20, Cat.neuter=TRUE, Cat.breed="Other", Cat.sex="male", Owner.sex="male", Cat.fur.color="Other", Cat.age=3))))
# Estimate Est.Error 2.5%ile 97.5%ile
# Australia 0.68 0.53 0.61 0.72
# Belarus 0.67 0.53 0.60 0.72
# Canada 0.68 0.52 0.63 0.71
# Czech Republic 0.67 0.53 0.60 0.72
# Finland 0.67 0.53 0.60 0.72
# France 0.68 0.53 0.61 0.72
# Germany 0.64 0.54 0.56 0.70
# India 0.66 0.54 0.58 0.71
# Ireland 0.67 0.53 0.60 0.72
# Italy 0.66 0.54 0.58 0.71
# Japan 0.68 0.53 0.61 0.72
# Latvia 0.67 0.53 0.59 0.72
# Netherlands 0.68 0.53 0.61 0.72
# New Zealand 0.67 0.53 0.60 0.72
# Panama 0.67 0.54 0.59 0.72
# Russia 0.65 0.54 0.57 0.71
# Slovenia 0.67 0.53 0.59 0.71
# Spain 0.66 0.54 0.58 0.71
# Sweden 0.68 0.53 0.62 0.72
# United Kingdom 0.69 0.52 0.64 0.72
# USA 0.71 0.51 0.68 0.72
# Vietnam 0.65 0.54 0.57 0.71The model-fitting shows that most of the covariates are unable to predict the catnip response and are best estimated with near-zero coefficients and that the splines are linear & also irrelevant; the only variables which appear to matter are the owner/country random effects, and being the first cat. This agrees with the meta-analysis finding age/sex/breed unhelpful but country important, and with my belief that some sort of bias is driving the anomalously high raw catnip rates: the first covariate is one of the strongest, and after adjusting for it, the catnip rate looks like it should. (The country-level estimates also look reasonably consistent with the GS survey, given their large uncertainties eg. USA is 71% here and 79% there.)
Since we can rule out most of the variables, it would be a lot easier to work with a subset of the variables (which also avoids missingness, raising the sample size from n = 288 to n = 351, giving a double boost of fewer irrelevant variables + more data):
c2 <- brm(Cat.response.Catnip ~ (1|ID) + (1|Owner.country) + First,
prior=c(prior(normal(0,0.3), class="sd"), prior(normal(0.66,0.1), class="Intercept")),
family=bernoulli(), iter=20000, data=catnip); summary(c2)
# ...Data: catnip (Number of observations: 351)
# Samples: 4 chains, each with iter = 20000; warmup = 10000; thin = 1;
# total post-warmup samples = 40000
#
# Group-Level Effects:
# ~ID (Number of levels: 218)
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sd(Intercept) 0.24 0.18 0.01 0.65 14720 1.00
#
# ~Owner.country (Number of levels: 23)
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# sd(Intercept) 0.64 0.15 0.37 0.97 25337 1.00
#
# Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Intercept 0.18 0.22 −0.25 0.60 40000 1.00
# FirstTRUE 0.93 0.31 0.33 1.53 40000 1.00
## Country-level posterior estimates:
re2 <- ranef(c2)$Owner.country
predictions <- round(digits=2, inv.logit(fitted(c2, data.frame(Cat.response.Catnip=NA, ID=1, Owner.country=row.names(re2), First=FALSE))))
cbind(Country=as.factor(row.names(re2)), as.data.frame(predictions))
# Country Estimate Est.Error 2.5%ile 97.5%ile
# 1 Australia 0.63 0.54 0.56 0.70
# 2 Austria 0.64 0.54 0.56 0.70
# 3 Belarus 0.64 0.54 0.56 0.70
# 4 Canada 0.66 0.53 0.61 0.70
# 5 Czech Republic 0.65 0.54 0.57 0.71
# 6 Finland 0.64 0.54 0.57 0.70
# 7 France 0.65 0.54 0.58 0.71
# 8 Germany 0.61 0.54 0.54 0.68
# 9 India 0.62 0.54 0.55 0.69
# 10 Ireland 0.64 0.54 0.56 0.70
# 11 Italy 0.63 0.54 0.55 0.69
# 12 Japan 0.65 0.54 0.57 0.71
# 13 Latvia 0.66 0.53 0.59 0.71
# 14 Netherlands 0.65 0.54 0.57 0.71
# 15 New Zealand 0.64 0.54 0.57 0.70
# 16 Panama 0.64 0.54 0.56 0.70
# 17 Russia 0.62 0.54 0.54 0.69
# 18 Slovenia 0.63 0.54 0.56 0.70
# 19 Spain 0.63 0.54 0.55 0.69
# 20 Sweden 0.66 0.53 0.59 0.71
# 21 United Kingdom 0.67 0.52 0.62 0.71
# 22 USA 0.69 0.51 0.66 0.71
# 23 Vietnam 0.62 0.54 0.54 0.69The First variable emerges beyond any doubt as a powerful bias in the results. The rest remains largely as before: heavy shrinkage around the common mean, as there’s insufficient data to estimate most countries with any reasonable accuracy (even the USA).
Intercorrelations of Catnip & Catnip Alternatives
Since the cat-level ratings will be affected by missingness as well, any attempt to correlate responses or extract a latent factor will be even more imprecise than the missingness percentages suggest. Still, we can look at the correlations and the tetrachoric correlations as well (since catnip response is treatable as a liability threshold model, it’s reasonable to imagine the other drugs likewise):
## Examine intercorrelations of the drug responses: simple Pearson's r, then more sophisticated tetrachoric correlation:
responses <- subset(catnip, select=c(Cat.response.Catnip, Cat.response.Valerian, Cat.response.Silvervine,
Cat.response.Thyme, Cat.response.Honeysuckle))
colnames(responses) <- c("Catnip", "Valerian", "Silvervine", "Thyme", "Honeysuckle")
round(digits=2, cor(use="pairwise.complete.obs", responses))
# Catnip Valerian Silvervine Thyme Honeysuckle
# Catnip 1.00
# Valerian 0.07 1.00
# Silvervine 0.13 0.71 1.00
# Thyme 0.25 0.72 1.00 1.00
# Honeysuckle 0.21 0.75 1.00 0.92 1.00
library(psych)
tc <- tetrachoric(responses); tc
# tetrachoric correlation
# Catnp Valrn Slvrv Thyme Hnysc
# Catnip 1.00
# Valerian 0.13 1.00
# Silvervine −0.18 0.68 1.00
# Thyme 0.36 0.76 0.84 1.00
# Honeysuckle 0.39 0.81 0.82 0.98 1.00
#
# with tau of
# Catnip Valerian Silvervine Thyme Honeysuckle
# −1.05 −0.41 0.67 0.29 0.27
## cutpoints for responder percentages reported:
round(digits=2, 1-pnorm(tc$tau))
# Catnip Valerian Silvervine Thyme Honeysuckle
# 0.85 0.66 0.25 0.39 0.40
fa(nfactors=1, responses)
# ...Warning: A Heywood case was detected.
# Standardized loadings (pattern matrix) based upon correlation matrix
# MR1 h2 u2 com
# Catnip 0.18 0.033 0.967 1
# Valerian 0.73 0.536 0.464 1
# Silvervine 1.00 1.003 −0.003 1
# Thyme 0.98 0.952 0.048 1
# Honeysuckle 0.98 0.969 0.031 1
#
# MR1
# SS loadings 3.49
# Proportion Var 0.70
# ...The correlations are interesting: there might be a cluster of Valerian/thyme/honeysuckle/silvervine responders, and then catnip is relatively unrelated. This might be connected to the demand bias - true catnip response data might show larger correlations. Factor analysis is not a good idea here, but if one extracts a single factor, it looks similar to the cluster. But these intercorrelations contrast with et al 2017, “Responsiveness of cats (Felidae) to silver vine (Actinidia polygama), Tatarian honeysuckle (Lonicera tatarica), valerian (Valeriana officinalis) and catnip (Nepeta cataria)”:
bol2017 <- read.csv("https://gwern.net/doc/cat/psychology/drug/catnip/2017-bol-cats.csv")
bol2017[,5:8] <- (bol2017[,5:8] > 0) # treat '5'/'10' (weak/strong response) as binary
bol2017Responses <- subset(bol2017, select=c("Catnip", "Valerian", "Silver.vine", "Tatarian.honeysuckle"))
colnames(bol2017Responses) <- c("Catnip", "Valerian", "Silvervine", "Honeysuckle") # rename for consistency
library(skimr)
skim(bol2017Responses)
# n obs: 100
# n variables: 4
#
# Variable type: logical
# variable missing complete n mean count
# Catnip 1 99 100 0.68 TRU: 67, FAL: 32, NA: 1
# Honeysuckle 3 97 100 0.53 TRU: 51, FAL: 46, NA: 3
# Silvervine 0 100 100 0.79 TRU: 79, FAL: 21, NA: 0
# Valerian 4 96 100 0.47 FAL: 51, TRU: 45, NA: 4
## calculate correlations & repeat factor analysis:
library(psych)
round(digits=2, cor(use="pairwise.complete.obs", bol2017Responses))
# Catnip Valerian Silvervine Honeysuckle
# Catnip 1.00
# Valerian 0.38 1.00
# Silvervine 0.14 0.26 1.00
# Honeysuckle 0.27 0.22 0.13 1.00
tetrachoric(bol2017Responses)
# Catnp Valrn Slvrv Hnysc
# Catnip 1.00
# Valerian 0.60 1.00
# Silvervine 0.24 0.47 1.00
# Honeysuckle 0.43 0.35 0.23 1.00
#
# with tau of
# Catnip Valerian Silvervine Honeysuckle
# −0.459 0.078 −0.806 −0.065
fa(bol2017Responses, nfactors=1)
# ...Standardized loadings (pattern matrix) based upon correlation matrix
# MR1 h2 u2 com
# Catnip 0.58 0.34 0.66 1
# Valerian 0.65 0.43 0.57 1
# Silvervine 0.32 0.10 0.90 1
# Honeysuckle 0.40 0.16 0.84 1
#
# MR1
# SS loadings 1.03
# Proportion Var 0.26
# ...But since the sample sizes are small, perhaps pooling the data for factor analysis (possible since we have individual-level data) will be helpful:
## Merge Bol et al 2017 + convenience sample data:
responsesAll <- merge(responses, bol2017Responses, all=TRUE)
## delete Thyme as causing too much missingness:
responsesAll$Thyme <- NULL
skim(responsesAll)
# Skim summary statistics
# n obs: 545
# n variables: 4
#
# Variable type: logical
# variable missing complete n mean count
# Catnip 40 505 545 0.83 TRU: 421, FAL: 84, NA: 40
# Honeysuckle 350 195 545 0.46 NA: 350, FAL: 106, TRU: 89
# Silvervine 375 170 545 0.61 NA: 375, TRU: 103, FAL: 67
# Valerian 347 198 545 0.48 NA: 347, FAL: 102, TRU: 96
round(digits=2, cor(use="pairwise.complete.obs", responsesAll))
# Catnip Valerian Silvervine Honeysuckle
# Catnip 1.00
# Valerian 0.21 1.00
# Silvervine −0.09 0.56 1.00
# Honeysuckle 0.16 0.54 0.53 1.00
tetrachoric(responsesAll)
# tetrachoric correlation
# Catnp Valrn Slvrv Hnysc
# Catnip 1.00
# Valerian 0.38 1.00
# Silvervine −0.16 0.82 1.00
# Honeysuckle 0.28 0.74 0.77 1.00
#
# with tau of
# Catnip Valerian Silvervine Honeysuckle
# −0.969 0.038 −0.269 0.109
fa(responsesAll, nfactors=1)
# Standardized loadings (pattern matrix) based upon correlation matrix
# MR1 h2 u2 com
# Catnip 0.13 0.018 0.98 1
# Valerian 0.78 0.610 0.39 1
# Silvervine 0.70 0.494 0.51 1
# Honeysuckle 0.73 0.528 0.47 1
#
# MR1
# SS loadings 1.65
# Proportion Var 0.41The combined data hints at a catnip vs non-catnip factor, but in general there are enough correlations that it may be possible to usefully include responses in deciding what to try: a non-response to catnip suggests trying silvervine next as silvervine response is common and may be inversely correlated with catnip response, while a catnip response would suggest valerian as an alternative if an owner wanted to mix things up or use during tolerance.
Human Consumption
For kicks, I added questions about human use of catnip as a herbal remedy. Catnip tea has been used to calm infants for centuries, among other things, and an old marijuana-related rumor claims you can get high off it (turns out that smoking catnip doesn’t work well).
catnipOld <- read.csv("https://gwern.net/doc/cat/psychology/drug/catnip/survey/2017-01-02-catnipsurvey-conveniencesample.csv")
catnipOld[!is.na(catnipOld$Owner.catnip.consumption) & catnipOld$Owner.catnip.consumption=="Wait, is this survey for me or my cat? I'm even more confused",]$Owner.catnip.consumption <- NA
library(qdapTools)
## split each string-list by comma-space delimiter, and unfold the list into a dataframe of dummy variables, one per food type:
catnipUse <- mtabulate(strsplit(as.character(catnipOld$Owner.catnip.consumption), ', '))
catnipUse$Rating <- catnipOld$Owner.catnip.consumption.efficacy
catnipUse <- catnipUse[!catnipUse$"NA",]
catnipUse <- catnipUse[!catnipUse$"FALSE",]
catnipUse$Smoked <- catnipUse$"Smelled burning catnip leaves" + catnipUse$"smoked catnip leaves"
catnipUse$Tea <- catnipUse$"valerian tea" + catnipUse$"catnip tea"
catnipUse$"NA" <- catnipUse$"FALSE" <- catnipUse$"Smelled burning catnip leaves" <- catnipUse$"smoked catnip leaves" <- catnipUse$"valerian tea" <- catnipUse$"catnip tea" <- NULL
colnames(catnipUse) <- c("Eaten.leaves.dry", "Eaten.leaves.fresh", "Skin.essential.oil", "Skin.leaves", "Eaten.leaves.food", "Rating", "Smoked", "Tea")
skim(catnipUse)
# Skim summary statistics
# n obs: 221
# n variables: 8
#
# Variable type: integer
# variable missing complete n mean sd p0 p25 p50 p75 p100 hist
# Eaten.leaves.dry 0 221 221 0.0045 0.067 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Eaten.leaves.food 0 221 221 0.0045 0.067 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Eaten.leaves.fresh 0 221 221 0.0045 0.067 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Rating 178 43 221 2.33 1.19 1 1 2 3 5 ▇▃▁▇▁▂▁▁
# Skin.essential.oil 0 221 221 0.0045 0.067 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Skin.leaves 0 221 221 0.0045 0.067 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Smoked 0 221 221 0.063 0.24 0 0 0 0 1 ▇▁▁▁▁▁▁▁
# Tea 0 221 221 0.1 0.31 0 0 0 0 1 ▇▁▁▁▁▁▁▁
colSums(catnipUse)
# Eaten.leaves.dry Eaten.leaves.fresh Skin.essential.oil Skin.leaves Eaten.leaves.food Rating Smoked
# 1 1 1 1 1 NA 14
# Tea
# 23
sort(decreasing=TRUE, colSums(mtabulate(strsplit(as.character(catnipOld$Owner.catnip.consumption.reason), ', '))))
# curiosity
# 15
# euphoria/getting high
# 9
# relaxation/sedation
# 9
# indigestion
# 2
# insomnia
# 2
# Experimenting
# 1
# headaches
# 1
# I like tea
# 1
# I like the taste
# 1
# i was under the age of 15 thinking it would get me NAbuzzedNA. It did nothing
# 1
# Just because
# 1
# Just to do it
# 1
# Mixed with lactation supplement
# 1
# NA
# 1
# stomach cramps
# 1
# Trying it out as a substitute/mixer for marijuana
# 1The “mixed with lactation supplement” reason throws me for a loop (how exactly does that work?), but the rest of the reasons make sense, although I’m a little surprised that the rumor of catnip getting you high is enough reason for quite a large fraction of catnip users to give it a try. (Perhaps catnip is much more accessible than a lot of other things, so people figure they might as well.)
Does the kind of catnip consumption affect the user’s estimate of how well it works? Using the 43 ratings, we can fit an ordinal regression model to the 1–5 Likert scale rating of efficacy against the method/kind of catnip consumption reported:
h <- brm(Rating ~ Eaten.leaves.dry + Eaten.leaves.fresh + Skin.essential.oil + Skin.leaves + Eaten.leaves.food + Smoked + Tea,
prior=c(set_prior("horseshoe(1, par_ratio=0.1)")), family=cumulative(), iter=20000, control=list(adapt_delta=0.9), data=catnipUse)
summary(h)
# Data: catnipUse (Number of observations: 43)
# Samples: 4 chains, each with iter = 20000; warmup = 10000; thin = 1;
# total post-warmup samples = 40000
#
# Population-Level Effects:
# Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
# Intercept[1] −0.79 0.44 −1.76 −0.02 21342 1.00
# Intercept[2] −0.02 0.40 −0.87 0.74 26825 1.00
# Intercept[3] 1.89 0.50 0.97 2.95 40000 1.00
# Intercept[4] 3.42 0.85 2.00 5.33 40000 1.00
# Eaten.leaves.dry 0.03 0.34 −0.45 0.87 35826 1.00
# Eaten.leaves.fresh 0.10 0.48 −0.32 1.60 23173 1.00
# Skin.essential.oil −0.03 0.33 −0.79 0.44 33813 1.00
# Skin.leaves −0.11 0.58 −1.67 0.33 21175 1.00
# Eaten.leaves.food 0.02 0.32 −0.49 0.78 38330 1.00
# Smoked −0.39 0.66 −2.13 0.07 10463 1.00
# Tea 0.08 0.27 −0.16 0.96 23907 1.00The most striking one is smoking, presumably because catnip doesn’t get you high. And it looks plausible that fresh leaves or tea are probably the best ways to get the relaxant effects.
-
One interesting issue with running the German version of the survey in Google Surveys was dealing with a bug in Google Translate (GT). I noticed while examining the suggested translations in GT that it was mistakenly translating both “I have a cat” and “I do not have a cat” to the same Germany sentence, Ich habe eine Katze, which translated back as the single sentence “I have a cat” (failing the roundtrip criteria of identity, that
En==En(De(En))); eine/Keine are the positive & negative German versions of “have”, so it was a major error. I thought nothing of it until GS refused to run the Germany survey, warning me that it needed editing so all respondents could answer the question, and suggesting that the response option “I have a cat” should be changed or a “NA” response added. Apparently GS automatically translates the non-English surveys back into English & checks that the responses are mutually exhaustive, so the first response was erroneously translated into English as “I have a cat” (rather than “I do not have a cat”) and the set of responses was indeed malformed (as all the responses then presume having a cat). After submitting a correction to GT & explaining this to the GS help desk, I was surprised & pleased they restarted the survey within a few minutes.↩︎