This is an interactive JS-based visualization of the difference in optimization potentials of a single-stage pipeline vs a multi-stage pipeline, in which new samples/measurements can be generated at each step (such as in evolutionary processes).
Because it optimizes over multiple steps, the multi-stage pipeline "ratchets upward" and can attain far more extreme maxima than a single-stage pipeline, even with the same total number of samples - the single-stage process quickly hits "diminishing returns", where large increases in sample count result in only small increases in the expected maximum. This means that small gains per stage, or a few stages, or a few generations of evolution, can result in large increases of sample means, compared to a single-stage process. Due to order statistics, the increases in means can cause larger increases in the probability of samples passing thresholds such as "top 1%"/≥2.32σ, or yielding extremes. And the more stages, the greater differences can be (single-stage selection increases logarithmically, while multi-stage increases linearly).
These increases can be counterintuitively large, but the gains/losses are relevant to understanding many processes, such as the clinical drug discovery pipeline (eg Scannell & Bosley 2016).
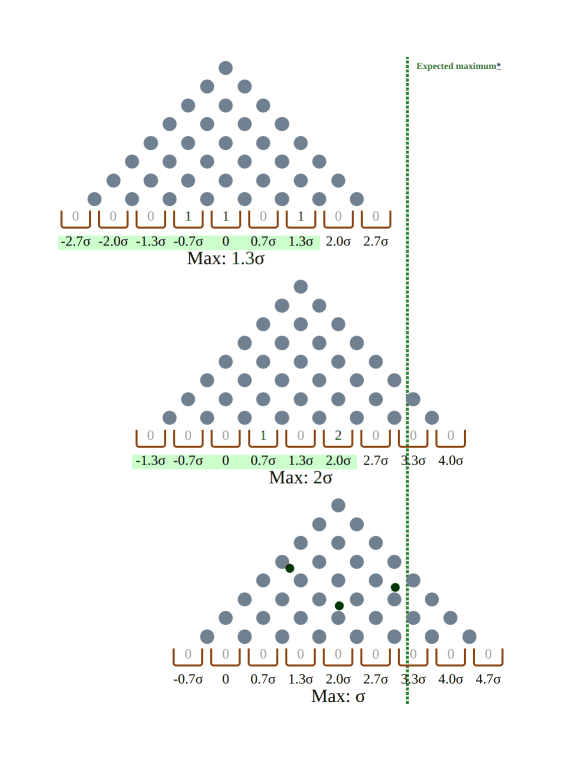
The visualization metaphor here is Francis Galton's quincunx or "bean machine": a ball (sample) falls from the top (zero-mean), and is affected by sets of pins (stochastic variables) which bounce the ball left/right with 50-50 probability (increase/decrease it) as it falls to the bottom (final total). The resulting binomial distribution approximates a normal distribution. The bean machine visually & concretely illustrates the sampling distribution of how a normally-distributed final variable can emerge out of the sum of many individual small discrete effects, without requiring any mathematics.
In this visualization, we generalize Galton's "bean machine" by allowing stacking of bean machines. To stack bean machines, we select the ball which is the maximum within each sample. How large is it? In the single-stage bean machine, selection stops there. In the multi-stage bean machine, another bean machine begins with the maximum serving as the seed & new average, and another round of generation & selection begins, and so on, until a final sample is selected, and we can see how large it is. The gains turn out to be larger the more samples we use total, unsurprisingly, but also the more stages we specify; the maximum possible maximum turns out to be when we have so many stages that there are just 2 samples per stage.